题目内容
如图,在⊙O中,弦AB与半径相等,连接OB并延长,使BC=OB.
(1)试判断直线AC与⊙O的位置关系,并证明你的结论;
(2)请你在⊙O上找到一个点D,使AD=AC(完成作图,证明你的结论),并求∠ABD的度数.

(1)试判断直线AC与⊙O的位置关系,并证明你的结论;
(2)请你在⊙O上找到一个点D,使AD=AC(完成作图,证明你的结论),并求∠ABD的度数.

(1)AC与⊙O相切.(1分)
证明:如图,∵AB与半径相等,即AB=OA=OB,
∴△OAB为等边三角形,
∴∠OAB=60°,∠OBA=60°.
∵BC=OB=AB,
∴∠BAC=∠C=30°,
∴∠OAC=90°,(2分)
∴AC与⊙O相切.
(2)延长BO交⊙O于D,连接AD,则必有AD=AC.(3分)
证明:∵∠BOA=60°,OA=OD,
∴∠D=30°.
又∵∠C=30°,
∴∠C=∠D,
∴AD=AC.(4分)
∵△OAB为等边三角形,
∴∠ABD=60°.(5分)
或作AD1⊥OC交⊙O于D1,交OC于E,连接BD1,则必有AD1=AC.(3分)
证明:∵∠C=30°,AD1⊥OC,
∴AE=
AC.
又∵AE=
AD1,
∴AC=AD1.(4分)
由OE⊥AD1,得到
=
,
∴∠BAD1=∠BD1A=
∠AOB=30°,
∴∠ABD1=120°.(5分)
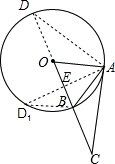
证明:如图,∵AB与半径相等,即AB=OA=OB,
∴△OAB为等边三角形,
∴∠OAB=60°,∠OBA=60°.
∵BC=OB=AB,
∴∠BAC=∠C=30°,
∴∠OAC=90°,(2分)
∴AC与⊙O相切.
(2)延长BO交⊙O于D,连接AD,则必有AD=AC.(3分)
证明:∵∠BOA=60°,OA=OD,
∴∠D=30°.
又∵∠C=30°,
∴∠C=∠D,
∴AD=AC.(4分)
∵△OAB为等边三角形,
∴∠ABD=60°.(5分)
或作AD1⊥OC交⊙O于D1,交OC于E,连接BD1,则必有AD1=AC.(3分)
证明:∵∠C=30°,AD1⊥OC,
∴AE=
| 1 |
| 2 |
又∵AE=
| 1 |
| 2 |
∴AC=AD1.(4分)
由OE⊥AD1,得到
 |
| AB |
 |
| BD1 |
∴∠BAD1=∠BD1A=
| 1 |
| 2 |
∴∠ABD1=120°.(5分)


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 AB=m.试求:
AB=m.试求:





