题目内容
【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为 ![]() BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )![]()
A.点E
B.点F
C.点M
D.点N
【答案】D
【解析】解:如图所示:
![]()
∵2AB=BC=3CD,
∴设CD=x,则BC=3x,AB=1.5x,
∵A、D两点表示的数分别为﹣5和6,
∴x+3x+1.5x=11,
解得:x=2,
故CD=2,BC=6,AB=3,
∵AC的中点为E,BD的中点为M,
∴AE=EC=4.5,BM=MD=4,
则E点对应的数字是﹣0.5,M对应的数字为:2,
∵BC之间距点B的距离为 ![]() BC的点N,
BC的点N,
∴BN= ![]() BC=2,
BC=2,
故AN=5,则N正好是原点.
所以答案是:D.
【考点精析】本题主要考查了数轴和两点间的距离的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记才能正确解答此题.

练习册系列答案
相关题目
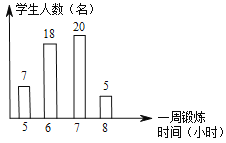
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
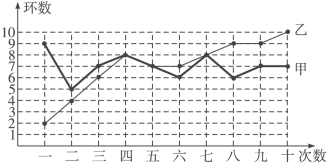
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环及以上的次数 | |
甲 | 7 | 1.2 | 1 | |
乙 | 5.4 |
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看;
②从平均数和中位数相结合看(分析谁的成绩好些);
③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).