Question

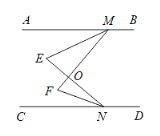
【题目】如图，AB∥CD，EM是∠AMF的平分线，NF是∠CNE的平分线，EN，MF交于点O.

（1）若∠AMF=50°，∠CNE=40°，∠E= °，∠F= °，∠MON= °；

（2）指出∠E，∠F与∠MON之间存在的等量关系，并证明．

Answer 1

【答案】（1）65；70；90 （2）∠E+∠F=∠MON；证明见解析

【解析】

（1）作EH∥AB，如图，利用平行线的性质得EH∥CD，则∠1＝∠AME，∠2＝∠CNE，于是得到∠MEN＝∠AME＋∠CNE，而∠AME＝∠AMF，所以∠MEN＝∠AMF＋∠CNE；同理可得∠F＝∠AMF＋∠CNE，∠MON＝∠AMF＋∠CNE；

（2）由（1）可知∠MON＝∠AMF＋∠CNE，∠E＝∠AMF＋∠CNE，∠F＝∠AMF＋∠CNE，求出∠E＋∠F即可得出结论．

解：（1）作EH∥AB，如图，

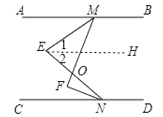
∵AB∥CD，

∴EH∥CD，

∴∠1＝∠AME，∠2＝∠CNE，

∴∠MEN＝∠1＋∠2＝∠AME＋∠CNE，

∵EM是∠AMF的平分线，

∴∠AME＝∠AMF，

∴∠MEN＝∠AMF＋∠CNE＝×50°＋40°＝65°；

同理可得：∠F＝∠AMF＋∠CNE＝50°＋×40°＝70°，

∠MON＝∠AMF＋∠CNE＝50°＋40°＝90°，

故答案为：65，70，90；

（2）∠E+∠F＝∠MON

证明：由（1）可知：∠MON＝∠AMF＋∠CNE，∠E＝∠AMF＋∠CNE，∠F＝∠AMF＋∠CNE，

∴∠E＋∠F＝（∠AMF＋∠CNE），

∴∠E+∠span>F＝∠MON．