Question

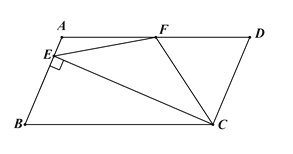
【题目】如图，在平行四边形 ABCD 中， AD 2 AB ；CF 平分 BCD 交 AD 于 F ，作 CE AB ， 垂足 E 在边 AB 上，连接 EF ．则下列结论：① F 是 AD 的中点； ② S△EBC 2S△CEF；③ EF CF ； ④ DFE 3AEF ．其中一定成立的是_____．（把所有正确结论的序号都填在横线上）

Answer 1

【答案】①③④.

【解析】

由角平分线的定义和平行四边形的性质可证得CD=DF，进一步可证得F为AD的中点，由此可判断①；延长EF，交CD延长线于M，分别利用平行四边形的性质以及①的结论可得△AEF≌△DMF，结合直角三角形的性质可判断③；结合EF=FM，利用三角形的面积公式可判断②；在△DCF和△ECF中利用等腰三角形的性质、外角的性质及三角形内角和可得出∠DFE=3∠AEF，可判断④，综上可得答案.

解：∵四边形ABCD为平行四边形，∴AD∥BC，

∴∠DFC=∠BCF，

∵CF平分∠BCD，∴∠BCF=∠DCF，

∴∠DFC=∠DCF，∴CD=DF，

∵AD=2AB，∴AD=2CD，

∴AF=FD=CD，即F为AD的中点，故①正确；

延长EF，交CD延长线于M，如图，

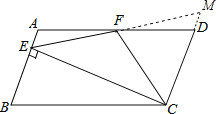
∵四边形ABCD是平行四边形，∴AB∥CD，

∴∠A=∠MDF，

∵F为AD中点，∴AF=FD，

又∵∠AFE=∠DFM，

∴△AEF≌△DMF（ASA），

∴FE=MF，∠AEF=∠M，

∵CE⊥AB，∴∠AEC=90°，

∴∠ECD=∠AEC=90°，

∵FM=EF，∴FC=FM，故③正确；

∵FM=EF，∴，

∵MC＞BE，

∴＜2，故②不正确；

设∠FEC=x，则∠FCE=x，

∴∠DCF=∠DFC=90°－x，

∴∠EFC=180°－2x，

∴∠EFD=90°－x+180°－2x=270°－3x ，

∵∠AEF=90°－x，

∴∠DFE=3∠AEF，故④正确；

综上可知正确的结论为①③④.

故答案为①③④.