题目内容
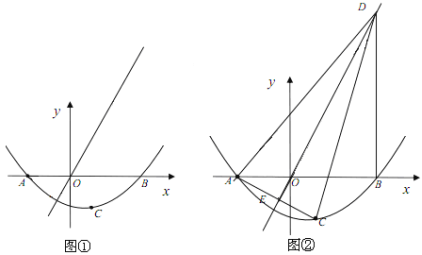
【题目】如图①,若二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数
的图象与x轴交于点A(-2,0),B(3,0)两点,点A关于正比例函数![]() 的图象的对称点为C。
的图象的对称点为C。
(1)求b、c的值;
(2)证明:点C 在所求的二次函数的图象上;
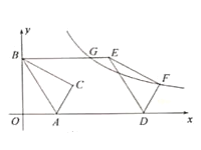
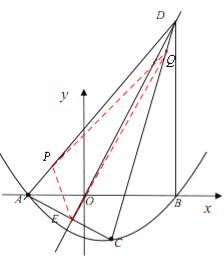
(3)如图②,过点B作DB⊥x轴交正比例函数![]() 的图象于点D,连结AC,交正比例函数
的图象于点D,连结AC,交正比例函数![]() 的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
的图象于点E,连结AD、CD。如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个到达终点时,另一个随之停止运动,连结PQ、QE、PE,设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,若存在,求出t的值;若不存在,请说明理由。
【答案】(1)![]() 。
。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入![]() 验证即可。
验证即可。
(3)存在时刻![]() ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。
【解析】
分析:(1)将A(-2,0),B(3,0)两点坐标 代入![]() ,即可求出b、c的值。
,即可求出b、c的值。
(2)利用轴对称和锐角三角函数求出点C的坐标,代入![]() 验证即可。
验证即可。
(3)通过证明△PAE∽△ECQ,求出时间t。
解:(1)∵二次函数![]() 的图象与x轴交于点A(-2,0),B(3,0)两点,
的图象与x轴交于点A(-2,0),B(3,0)两点,
∴ ,解得
,解得 。
。
∴![]() 。
。
(2)证明:由(1)得二次函数解析式为![]() 。
。
在正比例函数![]() 的图象上取一点F
的图象上取一点F![]() ,作FH⊥x轴于点H,则
,作FH⊥x轴于点H,则
![]() 。∴
。∴![]() 。
。
连接AC交 ![]() 的图象于点E,作CK 垂直x轴于点K,
的图象于点E,作CK 垂直x轴于点K,

∵点A关于![]() 的图象的对称点为C,
的图象的对称点为C,
∴OE垂直平分AC。
∵![]() ,OA=2,
,OA=2,
∴![]() 。
。
在Rt△ACK中,∵![]() ,
,
∴![]() 。∴
。∴![]() 。
。
∴点C 的坐标为![]() 。
。
将C ![]() 代入
代入![]() ,左边=右边,
,左边=右边,
∴点C在所求的二次函数的图象上。
(3)∵DB⊥x轴交![]() 的图象于点D,B(3,0),
的图象于点D,B(3,0),
∴把x=3代入![]() 得
得![]() ,即BD=
,即BD=![]() 。
。
在Rt△ACK中,![]() ,
,
∵OE垂直平分AC,
∴![]() ,
,![]() 。
。
假设存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,
则![]() 。
。
∵![]() , ∴
, ∴![]() 。
。
又∵![]() ,∴
,∴![]() 。
。
又∵![]() ,∴△PAE∽△ECQ。∴
,∴△PAE∽△ECQ。∴![]() ,即
,即![]() 。
。
整理,得![]() ,解得
,解得![]() (不合题意,舍去)。
(不合题意,舍去)。
∴存在时刻![]() ,使PE平分∠APQ,同时QE平分∠PQC。
,使PE平分∠APQ,同时QE平分∠PQC。

【题目】一分钟投篮测试规定,得6分以上为合格,得9分以上为优秀,甲、乙两组同学的一次测试成绩如下:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上述统计数据,把下面的图和表补充完整;

一分钟投篮成绩统计分析表:
统计量 | 平均分 | 方差 | 中位数 | 合格率 | 优秀率 |
甲组 | 2.56 | 6 | 80.0% | 26.7% | |
乙组 | 6.8 | 1.76 | 86.7% | 13.3% |
(2)下面是小明和小聪的一段对话,请你根据(1)中的表,写出两条支持小聪的观点的理由.