题目内容
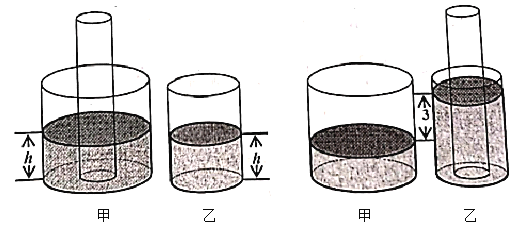
【题目】如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体, 甲、乙容器的内底面半径分别为![]() 和
和![]() ,现将一个半径为
,现将一个半径为![]() 的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为
的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为![]() (如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高
(如图甲),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高![]() (如图乙).
(如图乙).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含![]() 的代数式表示).
的代数式表示).
(3)求![]() 的值.
的值.
【答案】(1) ![]() 和
和![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】
(1)根据题意甲、乙容器的内底面半径,即可求甲、乙两个容器的内底面面积;
(2)由题意用含![]() 的代数式表示甲容器内液体的体积即可;
的代数式表示甲容器内液体的体积即可;
(3)根据题意乙容器的液面比甲容器的液面高![]() ,建立含
,建立含![]() 的等量关系式,并求解即可.
的等量关系式,并求解即可.
解:(1) 由甲、乙容器的内底面半径分别为![]() 和
和![]() ;
;
可知甲、乙两个容器的内底面面积分别为![]() 和
和![]() .
.
(2)由题意可知甲容器内液体的体积为![]() =
=![]()
![]() .
.
(3)由题意可知乙的液体体积不变以此建立方程得:![]() ,
,
解得![]() .
.

练习册系列答案
相关题目