Question

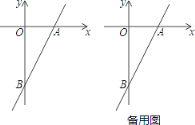
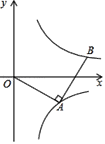
【题目】如图，OA＝AB，∠OAB＝90°，双曲线y＝经过点A，双曲线y＝﹣经过点B，已知点A的纵坐标为﹣2，则点B的坐标为_____．

Answer 1

【答案】

【解析】

作AC⊥y轴于C，BD⊥AC于D，如图，设A（-，-2），则AC=-，OC=2，证明△AOC≌△BAD得到BD=AC=-，AD=OC=2，则B（-+2，--2），然后把B（-+2，--2）代入y=-得（-+2）（--2）=-k，然后解关于k的方程即可得到B点坐标．

作AC⊥y轴于C，BD⊥AC于D，如图，

设A（-，-2），则AC=-，OC=2，

∵∠OAB=90°，∠OCA=90°，

∴∠OAC+∠BAD=90°，∠OAC+∠AOC=90°，

∴∠AOC=∠BAD，

在△AOC和△BAD中，

，

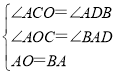∴△AOC≌△BAD（AAS），

∴BD=AC=-，AD=OC=2，

∴B（-+2，--2），

把B（-+2，--2）代入y=-得（-+2）（--2）=-k，

整理得k2+4k-16=0，解得k1=2-2（舍去），k2=-2-2，
∴B点坐标为（3+，-1）．

故答案为（3+，-1）．