题目内容
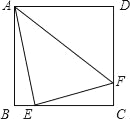
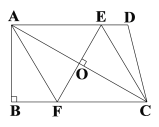
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由于知道了EF垂直平分AC,因此只要证出四边形AFCE是平行四边形即可得出AFCE是菱形的结论.
(2)根据勾股定理得出AC,进而利用勾股定理解答即可.
证明:(1)∵EF是对角线AC的垂直平分线,
∴AO=CO,AC⊥EF,
∵AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
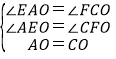 ,
,
∴△AEO≌△CFO(AAS),
∴AE=CF,
∴四边形AFCE是平行四边形,
又∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠B=90°,AB=6,BC=8,
∴AC= ![]() ,
,
∵四边形AFCE是菱形,
∴AF=FC,
在Rt△ABF中,设AF=FC=x,则BF=8-x
∴AB2+BF2=AF2,
∴62+(8-x)2=x2,
∴x=![]() ,
,
∴OF ![]() ,
,
∴EF=2OF=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目