题目内容
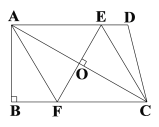
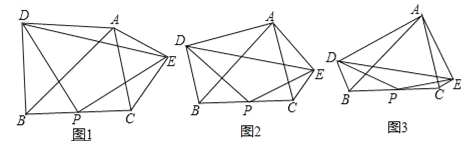
【题目】已知在△ABC中,∠BAC=60°,点P为边BC的中点,分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE,且∠DAB=∠EAC=α,连结PD,PE,DE.
(1)如图1,若α=45°,则![]() = ;
= ;
(2)如图2,若α为任意角度,求证:∠PDE=α;
(3)如图3,若α=15°,AB=8,AC=6,则△PDE的面积为 .
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1) 分别取AB、AC中点F、G,连接DF、PF、PG、EG,证明AFPG为平行四边形,再证明△DFP和△PGE全等,再证明∠DPE=90°,最后得到△DEP是等腰直角三角形.
(2)类似(1)证明四边形AFPG为平行四边形,证明△DFP和△PGE全等,再证明∠DPE=180°﹣∠DFB,∠DFA=180°﹣∠DFB,所以∠DPE=∠DFA,所以等腰三角形DPE和等腰三角形ADF中,∠PDE=∠DAF=α.
(3)同理(1)求出DP=EP长度,由(2)可得,∠PDE=α=15°=∠PED,过点E作DP的垂线,交DP的延长线于H,则∠EPH=30°,所以可求得EH= ![]() PE=
PE= ![]() ,所以可以得到△PDE的面积.
,所以可以得到△PDE的面积.
试题分析:
解:(1)分别取AB、AC中点F、G,连接DF、PF、PG、EG,则根据三角形中位线定理可得,AF=PG,AG=PF,即四边形AFPG为平行四边形,
∴∠PFB=∠BAC=∠PGC=60°,∵Rt△ABD和Rt△ACE中,∠DAB=∠EAC=α=45°,
∴△ABD和△ACE都是等腰直角三角形,∴DF⊥AB,EG⊥AC,且DF=AF=PG,PF=AG=EG,∴∠DFP=∠PGE=150°,
在△DFP和△PGE中, 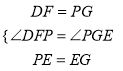 ,
,
∴△DFP≌△PGE(SAS),
∴DP=PE,∠GPE=∠FDP,
∵△DPF中,∠FDP+∠DPF+∠PFB=90°,而∠PFB=∠FPG,
∴∠GPE+∠DPF+∠FPG=90°,即∠DPE=90°,
∴△DEP是等腰直角三角形,∴![]() .
.
(2)证明:分别取AB、AC中点F、G,连接DF、PF、PG、EG,则根据三角形中位线定理可得,AF=PG,AG=PF,即四边形AFPG为平行四边形,
∴∠PFB=∠BAC=∠PGC=60°,∵Rt△ABD和Rt△ACE中,DF=AF,GE=AG,∴DF=PG,PF=EG,∠DFB=2∠DAF=2α,∠EGC=2∠CAE=2α,
∴∠DFP=∠PGE,在△DFP和△PGE中, 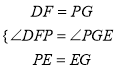 ,
,
∴△DFP≌△PGE(SAS),∴DP=PE,∠GPE=∠FDP,
∵在△DFP中,∠FDP+∠DPF+∠PFB=180°﹣∠DFB,而∠PFB=∠FPG,∴∠GPE+∠DPF+∠FPG=180°﹣∠DFB,即∠DPE=180°﹣∠DFB,
又∵∠DFA=180°﹣∠DFB,∴∠DPE=∠DFA,
∴在等腰三角形DPE和等腰三角形ADF中,∠PDE=∠DAF=α.
(3)分别取AB、AC中点F、G,连接DF、PF、PG、EG,则根据三角形中位线定理可得,AF=PG=4,AG=PF=3,即四边形AFPG为平行四边形,∴∠PFB=∠BAC=∠PGC=60°,
∵Rt△ABD和Rt△ACE中,DF=AF,GE=AG,∴DF=PG=4,PF=EG=3,∠DFB=2∠DAF=2α=30°,∠EGC=2∠CAE=2α=30°,∴∠DFP=∠PGE=90°,
∴DP=EP= ![]() =5,
=5,
由(2)可得,∠PDE=α=15°=∠PED,过点E作DP的垂线,交DP的延长线于H,则∠EPH=30°,∴EH= ![]() PE=
PE= ![]() ,∴△PDE的面积=
,∴△PDE的面积= ![]() ×DP×EH=
×DP×EH= ![]() ×5×
×5×![]() =
= ![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案