题目内容
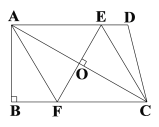
【题目】如图,点![]() 、
、![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 上的点,且
上的点,且![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ,其中一定正确的有( )
,其中一定正确的有( )

A. 0个B. 1个C. 2个D. 3个
【答案】C
【解析】
根据正方形的性质,运用SAS证明△ABF≌△DAE,运用全等三角形性质逐一解答.
∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,∴AF=DE.
∴△ABF≌△DAE.
∴AE=BF;∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,
即AE⊥BF,故①正确;
若AO=OE,则BO垂直平分AE,
∴AB=BC=BE,这与BE>BC矛盾,故②不正确;
S△AOB=S△ABF-S△AOF,S四边形DEOF=S△ADE-S△AOF,
∵△ABF≌△DAE,
∴S△ABF=S△ADE,
∴S△AOB=S四边形DEOF,故③正确.
故选C.

练习册系列答案
相关题目