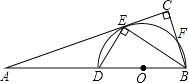
题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,将线段
,将线段![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位,得到线段
个单位,得到线段![]() ,
,![]() 恰好都落在反比例函数
恰好都落在反比例函数![]() 的图象上.
的图象上.
(1)用含![]() 的代数式表示点
的代数式表示点![]() ,
,![]() 的坐标;
的坐标;
(2)求![]() 的值和反比例函数
的值和反比例函数![]() 的表达式;
的表达式;
(3)点![]() 为反比例函数
为反比例函数![]() 图象上的一个动点,直线
图象上的一个动点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,请直接写出点
,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]()
![]() ;
; ![]()
![]() ;(2)n=6;
;(2)n=6;![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)利用平移的性质,可用含![]() 的代数式表示点
的代数式表示点![]() ,
,![]() 的坐标;
的坐标;
(2)根据点![]() ,
,![]() 的坐标,利用待定系数法可得出关于
的坐标,利用待定系数法可得出关于![]() ,
,![]() 的方程组,解之即可得出结论;
的方程组,解之即可得出结论;
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,利用相似三角形的性质可得出
,利用相似三角形的性质可得出![]() 的值,再利用反比例函数图象上点的坐标特征可求出点
的值,再利用反比例函数图象上点的坐标特征可求出点![]() 的坐标.
的坐标.
(1)∵点![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位得到点
个单位得到点![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
同理,可得出:点![]() 的坐标为
的坐标为![]() .
.
(2)将![]() ,
,![]() 代入
代入![]() ,得:
,得:
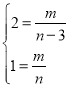 ,解得:
,解得:![]() ,
,
∴![]() 的值为6,反比例函数的表达式为
的值为6,反比例函数的表达式为![]() .
.
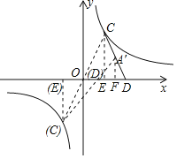
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点F,如图所示.
轴于点F,如图所示.
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
当![]() 时,
时,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() .
.
综上所述:点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目