题目内容
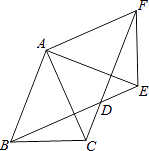
【题目】如图.在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.

【答案】(1)△ODE是等边三角形;理由见解析;(2)BD=DE=EC,理由见解析;
【解析】
试题(1)根据平行线的性质及等边三角形的性质可得到△ODE是等边三角形;
(2)根据角平分线的性质及平行线的性质可得到∠DBO=∠DOB,根据等角对等边可得到DB=DO,同理可证明EC=EO,因为DE=OD=OE,所以BD=DE=EC.
试题解析:(1)△ODE是等边三角形,
其理由是:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°
∴△ODE是等边三角形;
(2)答:BD=DE=EC,
其理由是:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°,
∵OD∥AB,
∴∠BOD=∠ABO=30°,
∴∠DBO=∠DOB,
∴DB=DO,
同理,EC=EO,
∵DE=OD=OE,
∴BD=DE=EC.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目