题目内容
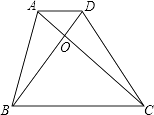
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) 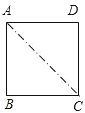

A.0.5cm
B.1cm
C.1.5cm
D.2cm
【答案】B
【解析】解答:设AC交A′B′于H , ∵∠A=45°,∠D=90°
∴△A′HA是等腰直角三角形
设AA′=x , 则阴影部分的底长为x , 高A′D=2-x
∴x(2-x)=1
∴x=1
即AA′=1cm.
故选:B.
分析:由平移的性质,结合阴影部分是平行四边形,△AA′H与△HCB′都是等腰直角三角形,则若设AA′=x , 则阴影部分的底长为x , 高A′D=2-x , 根据平行四边形的面积公式列出方程求解.解答此题的关键是抓住平移后图形的特点,利用方程方法解题.

练习册系列答案
相关题目