题目内容
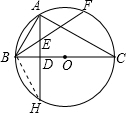
如图，已知Rt△ABC是⊙O的内接三角形，∠BAC=90°，AH⊥BC，垂足为D，过点B作弦BF交AD于点
E，交⊙O于点F，且AE=BE．
（1）求证：
=
；
（2）若BE•EF=32，AD=6，求BD的长．
E，交⊙O于点F，且AE=BE．（1）求证：
 |
| AB |
|
| AF |
（2）若BE•EF=32，AD=6，求BD的长．
（1）证明：连接BH，
根据垂径定理可知弧AB=弧BH，
∴∠BAH=∠BHA．
∵AE=BE，
∴∠BAH=∠ABF．
∴∠BHA=∠ABF．
∴
=
．
（2）∵BE•EF=32，
∴AE•EH=32．
∵AD=6，
∴AH=12．
∴AE•（12-AE）=32．
解得AE=4或8，
从图中可知AE=4，DE=2
∵AE=BE，
∴BE=4．
∴BD=
=2
．
根据垂径定理可知弧AB=弧BH，
∴∠BAH=∠BHA．
∵AE=BE，
∴∠BAH=∠ABF．
∴∠BHA=∠ABF．
∴
|
| AB |
|
| AF |
（2）∵BE•EF=32，
∴AE•EH=32．
∵AD=6，
∴AH=12．
∴AE•（12-AE）=32．
解得AE=4或8，
从图中可知AE=4，DE=2
∵AE=BE，
∴BE=4．
∴BD=
| 42-22 |
| 3 |
练习册系列答案
相关题目
