题目内容
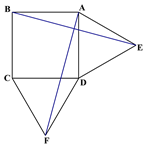
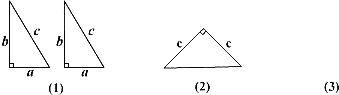
【题目】如图(1)是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为
和
斜边长为
图(2)是以
为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个直角梯形.
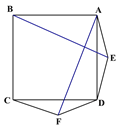
(1)在图(3)处画出拼成的这个图形的示意图；
(2)利用(1)画出的图形证明勾股定理.
【答案】(1)见解析；(2)证明见解析.
【解析】
(1)此题要由图中给出的三个三角形组成一个梯形，而且上底和下底分别为a，b，高为a+b；
(2)利用梯形的面积和三角形的面积公式列出等式即可求出勾股定理.
(1)如图所示；
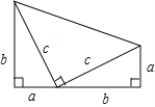
(2)由图我们根据梯形的面积公式可知，
梯形的面积=
(a+b)(a+b)，
从图中我们还发现梯形的面积=三个三角形的面积，即ab+ab+c2，
所以(a+b)(a+b)=ab+ab+c2，
∴a2+b2=c2.
名校课堂系列答案
【题目】A、B两地果园分别有橘子40吨和60吨，C、D两地分别需要橘子30吨和70吨；已知从A、B到C、D的运价如表：
到C地 | 到D地 | |
A果园 | 每吨15元 | 每吨12元 |
B果园 | 每吨10元 | 每吨9元 |
（1）若从A果园运到C地的橘子为x吨，则从A果园运到D地的橘子为 吨，从A果园将橘子运往D地的运输费用为 元.
（2）用含x的式子表示出总运输费（要求：列式、化简）
（3）若这批橘子在C地和D地进行再加工，经测算，全部橘子加工完毕后总成本为w元，且
.则当x= 时，w有最 值（填“大”或“小”），这个值是 .
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
学生最喜欢的活动项目的人数统计表
项目 | 学生数（名） | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息，解答下列问题：
（1）m= ，n= ，p= ；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
【题目】用火柴棒按下列方式搭建三角形：
（1）填表：
三角形个数 | 1 | 2 | 3 | 4 | … |
火柴棒根数 | … |
（2）当三角形的个数为
时，火柴棒的根数是多少？
（3）求当
时，有多少根火柴棒？
（4）当火柴棒的根数为2017时，三角形的个数是多少？
