Question

【题目】有一块直角三角形的绿地，量得两直角边长分别为6m和8m，现在要将绿地扩充成等腰三角形，且扩充部分是以8m为直角边的直角三角形，求扩充后等腰三角形绿地的周长.

Answer 1

【答案】扩充后的绿地周长为32m或（20+4）m或m.

【解析】

根据题意画出图形，构造出等腰三角形，根据等腰三角形及直角三角形的性质利用勾股定理解答.

在Rt△ABC中，∠ACB=90°，AC=8，BC=6

由勾股定理有：AB=10，应分以下三种情况：

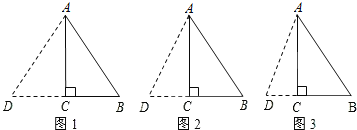
①如图1，当AB=AD=10时，

∵AC⊥BD，

∴CD=CB=6m，

∴△ABD的周长=10+10+2×6=32m；

②如图2，当AB=BD=10时，

∵BC=6m，

∴CD=10-6=4m，

∴AD==4m，

∴△ABD的周长=10+10+4=(20+4)m；

③如图3，当AB为底时，设AD=BD=x，则CD=x-6，

由勾股定理得：AD2=AC2+CD2，

即82+(x-6)2=x2，

解得，x=，

∴△ABD的周长为：AD+BD+AB=++10=m，

综上可知，扩充后的绿地周长为32m或(20+4)m或m.