题目内容
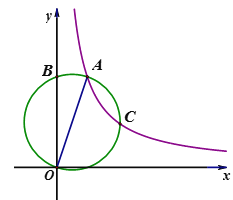
【题目】如图，点A在反比例函数图象
上运动，以线段OA为直径的圆交该双曲线于点C，交y轴于点B，若弧CB=弧CO，则点A的坐标为____。
【答案】
【解析】
连接AB,AC,BC,OC,过点C作CD⊥y轴于点D.再运用勾股定理得到
，又因为弧CB=弧CO，得到CB=CO，设设A的坐标为
，则
，
，求得C点坐标，然后代入，求出m，即可确定A点坐标.
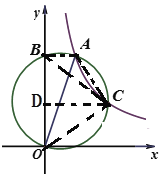
解：如图，连接AB,AC,BC,OC,过点C作CD⊥y轴于点D.
∵AB是圆O的直径，
∴∠ABO=∠ACO=90°
∴
∴
∵弧CB=弧CO
∴OC=BC
又CD⊥y轴于点D，
∴BD=OD
设A的坐标为，则，
又∵CD⊥y轴于点D，且点C在
的图象上，
∴C的坐标为（2m，
）
∴
，
化简得:，
即
，
解得
（舍去），
则A的坐标为
故答案为：
练习册系列答案
相关题目
