题目内容
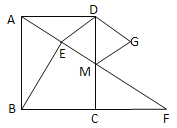
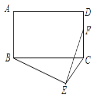
【题目】如图，在矩形ABCD中，AB=6，AD=8，以BC为斜边在矩形所在平面作直角三角形BEC，F为CD的中点，则EF的最小值为 （ ）
A. 
B. 4C. 
D. 1
【答案】D
【解析】
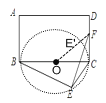
由圆周角定理可知点E在以BC为直径的⊙O上，所以当O，E’，F三点共线时，E’F取最小值，然后求出OF，OE’即可解决问题.
解：由题意可知：∠BEC=90°，
∴点E在以BC为直径的⊙O上，连结OF，如图，则当O，E’，F三点共线时，E’F取最小值，
∵四边形ABCD是矩形，
∴BC=AD=8，CD=AB=6，
∵BC为直径，F为CD的中点，
∴OC=4，CF=3，OE’=4，
∴OF=
，
∴E’F=OF- OE’=5-4=1，即EF的最小值为1，
故选：D.
练习册系列答案
相关题目
