Question

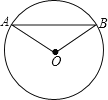
【题目】如图，在⊙O中，弦AB＝2cm，∠AOB＝120°，则⊙O的半径为_____cm．

Answer 1

【答案】2．

【解析】

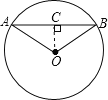
过O作OC⊥AB，构建Rt△AOC，利用垂径定理及勾股定理解题即可.

过O作OC⊥AB，垂足为C，如图所示：

∵OC⊥AB，且AB＝cm，

∴AC＝BC＝AB＝cm，

又∵OA＝OB，OC⊥AB，

∴OC为∠AOB的平分线，∠AOB＝120°

∴∠AOC＝∠BOC＝ ∠AOB＝60°，

在Rt△AOC中，∠ACO＝90°，∠AOC＝60°，

∴∠A＝30°，

设OC＝xcm，则有OA＝2xcm，

根据勾股定理得：AC2+OC2＝OA2，即3+x2＝4x2，

解得：x＝1，或x＝﹣1（舍去），

则半径OA＝2x＝2cm．

故答案为：2．