题目内容
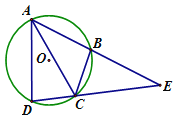
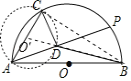
【题目】如图,AB是半圆O的直径,点C在半圆O上,AB=4cm,∠CAB=60°,P是弧![]() 上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是_____.
上的一个动点,连接AP,过C点作CD⊥AP于D,连接BD,在点P移动的过程中,BD的最小值是_____.

【答案】(![]() ﹣1)cm
﹣1)cm
【解析】
以AC为直径作圆O′,连接BO′、BC.在点P移动的过程中,点D在以AC为直径的圆上运动,当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D,利用勾股定理求出BO′即可解决问题.
如图,以AC为直径作圆O′,连接BO′、BC.
∵CD⊥AP,
∴∠ADC=90°,
∴在点P移动的过程中,点D在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AB=4cm,∠CAB=60°,
∴BC=ABsin60°=2![]() ,AC=ABcos60°=2cm.
,AC=ABcos60°=2cm.
在Rt△BCO′中,BO′=![]() ,
,
∵O′D+BD≥O′B,
∴当O′、D、B共线时,BD的值最小,最小值为O′B﹣O′D=![]() ﹣1,
﹣1,
故答案为(![]() ﹣1)cm.
﹣1)cm.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目