题目内容
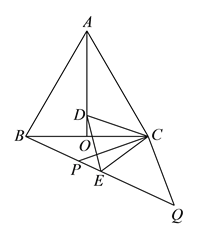
【题目】(本题10分)如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=![]() ,DE=3.
,DE=3.

求:(1)⊙O的半径;(2)弦AC的长;(3)阴影部分的面积.
【答案】(1)6; (2)6; (3) ![]()
【解析】试题分析:(1)半径OD⊥BC,所以由垂径定理知:CE=BE,在直角△OCE中,根据勾股定理就可以求出OC的值;
(2)根据AB是⊙O的直径,得到∠ACB=90°,因而在直角三角形ABC中根据勾股定理得到AC的长;
(3)阴影部分的面积就是扇形OCA的面积减去△OAC的面积.
试题解析:解:(1)∵半径OD⊥BC,∴CE=BE,∵BC=![]() ,∴CE=
,∴CE=![]() ,设OC=x,在直角三角形OCE中,OC2=CE2+OE2,∴x2=(
,设OC=x,在直角三角形OCE中,OC2=CE2+OE2,∴x2=(![]() )2+(x﹣3)2,∴x=6,即半径OC=6;
)2+(x﹣3)2,∴x=6,即半径OC=6;
(2)∵AB为直径,∴∠ACB=90°,AB=12,又∵BC=![]() ,∴AC2=AB2﹣BC2=36,∴AC=6;(3)∵OA=OC=AC=6,∴∠AOC=60°,∴S阴=S扇﹣S△OAC=
,∴AC2=AB2﹣BC2=36,∴AC=6;(3)∵OA=OC=AC=6,∴∠AOC=60°,∴S阴=S扇﹣S△OAC=![]() ﹣
﹣![]()
=![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目