ĚâÄżÄÚČÝ
ĄžĚâÄżĄżÎŇĂÇĐÂś¨ŇĺŇťÖÖČý˝ÇĐÎŁşČôŇť¸öČý˝ÇĐÎÖĐ´ćÔÚÁ˝ąßľÄĆ˝ˇ˝˛îľČÓÚľÚČýąßÉϸ߾ÄĆ˝ˇ˝ŁŹÔňłĆŐâ¸öČý˝ÇĐÎÎŞš´šÉ¸ßČý˝ÇĐÎŁŹÁ˝ąß˝ťľăÎŞš´šÉśĽľăŁŽ
ĄńĚŘŔý¸ĐÖŞ
˘ŮľČŃüÖą˝ÇČý˝ÇĐÎ š´šÉ¸ßČý˝ÇĐÎŁ¨ÇëĚîĐ´Ą°ĘÇĄąťňŐߥ°˛ťĘÇĄąŁŠŁť
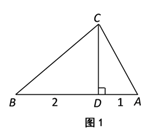
˘ÚČçÍź1ŁŹŇŃÖŞĄ÷ABCÎŞš´šÉ¸ßČý˝ÇĐÎŁŹĆäÖĐCÎŞš´šÉśĽľăŁŹCDĘÇABąßÉϾĸߣŽČô![]() ŁŹĘÔÇóĎßśÎCDľÄł¤śČŁŽ
ŁŹĘÔÇóĎßśÎCDľÄł¤śČŁŽ
ĄńÉîČëĚ˝žż
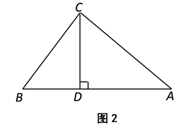
ČçÍź2ŁŹŇŃÖŞĄ÷ABCÎŞš´šÉ¸ßČý˝ÇĐÎŁŹĆäÖĐCÎŞš´šÉśĽľăÇŇCAŁžCBŁŹCDĘÇABąßÉϾĸߣŽĘÔĚ˝žżĎßśÎADÓëCBľÄĘýÁżšŘĎľŁŹ˛˘¸řÓčÖ¤Ă÷Łť
ĄńÍĆšăÓŚÓĂ
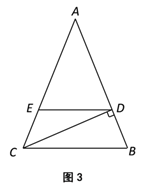
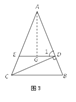
ČçÍź3ŁŹľČŃüĄ÷ABCÎŞš´šÉ¸ßČý˝ÇĐÎŁŹĆäÖĐ![]() ŁŹCDÎŞABąßÉϾĸߣŹšýľăDĎňBCąßŇýĆ˝ĐĐĎßÓëACąß˝ťÓÚľăEŁŽČô
ŁŹCDÎŞABąßÉϾĸߣŹšýľăDĎňBCąßŇýĆ˝ĐĐĎßÓëACąß˝ťÓÚľăEŁŽČô![]() ŁŹĘÔÇóĎßśÎDEľÄł¤śČŁŽ
ŁŹĘÔÇóĎßśÎDEľÄł¤śČŁŽ
Ąž´đ°¸ĄżĄńĚŘŔý¸ĐÖŞ:˘ŮĘÇŁť˘Ú![]() Łť
Łť
ĄńÉîČëĚ˝žżŁş ![]() ŁŹŔíÓÉźű˝âÎöŁť
ŁŹŔíÓÉźű˝âÎöŁť
ĄńÍĆšăÓŚÓĂŁş2aŁŽ
Ąž˝âÎöĄżĘÔĚâˇÖÎöŁşĄńĚŘŔý¸ĐÖŞ
˘Ů¸ůžÝš´šÉ¸ßČý˝ÇĐξĜ¨Ňĺ˝řĐĐĹМϟ´żÉ.
˘ÚÉč![]() ¸ůžÝš´šÉś¨ŔíżÉľĂŁş
¸ůžÝš´šÉś¨ŔíżÉľĂŁş ![]() ŁŹ¸ůžÝš´šÉ¸ßČý˝ÇĐξĜ¨ŇĺÁĐłöˇ˝łĚŁŹ˝âˇ˝łĚź´żÉ.
ŁŹ¸ůžÝš´šÉ¸ßČý˝ÇĐξĜ¨ŇĺÁĐłöˇ˝łĚŁŹ˝âˇ˝łĚź´żÉ.
ĄńÉîČëĚ˝žż
¸ůžÝš´šÉ¸ßČý˝ÇĐξĜ¨Ňĺ˝áşĎš´šÉś¨Ŕíź´żÉľĂłöËüĂÇÖŽźäľÄšŘĎľ.
ĄńÍĆšăÓŚÓĂ
ÔËÓĂĚ˝žżľÄ˝ášű˝řĐĐÔËËăź´żÉ.
ĘÔĚâ˝âÎöŁş
ĄńĚŘŔý¸ĐÖŞ
˘Ů ĘÇ Łť
˘ÚÉč![]()
¸ůžÝš´šÉś¨ŔíżÉľĂŁş ![]() ŁŹ
ŁŹ
ÓÚĘÇ![]() ŁŹ
ŁŹ
Ąŕ![]() Łť
Łť
ĄńÉîČëĚ˝žż
ÓÉ![]() żÉľĂŁş
żÉľĂŁş ![]() ŁŹśř
ŁŹśř![]() ŁŹ
ŁŹ
Ąŕ![]() ŁŹź´
ŁŹź´![]() Łť
Łť

ĄńÍĆšăÓŚÓĂ
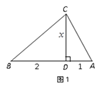
šýľăAĎňEDŇý´šĎߣŹ´š×ăÎŞGŁŹ
ĄßĄ°š´šÉ¸ßČý˝ÇĐÎĄąĄ÷ABCÎŞľČŃüČý˝ÇĐÎŁŹÇŇ![]() ŁŹ
ŁŹ
ĄŕÖťÄÜĘÇ![]() ŁŹÓÉÉĎÎĘżÉÖŞ
ŁŹÓÉÉĎÎĘżÉÖŞ![]() ĄĄ˘ŮŁŽ
ĄĄ˘ŮŁŽ
ÓÖEDĄÎBCŁŹĄŕ![]() ĄĄ˘ÚŁŽ
ĄĄ˘ÚŁŽ
śř![]() ĄĄ˘ŰŁŹ
ĄĄ˘ŰŁŹ
ĄŕĄ÷AGDĄŐĄ÷CDBŁ¨AASŁŠŁŹÓÚĘÇ![]() ŁŽ
ŁŽ
Ň×ÖŞĄ÷ADEÓëĄ÷ABCžůÎŞľČŃüČý˝ÇĐÎŁŹ
¸ůžÝČýĎßşĎŇťÔŔíżÉÖŞ![]() ŁŽ
ŁŽ
ÓÖ![]() Ąŕ
Ąŕ![]() ŁŹ
ŁŹ
Ąŕ![]() ŁŽ
ŁŽ

 ĂűĐŁżÎĚĂĎľÁĐ´đ°¸
ĂűĐŁżÎĚĂĎľÁд𰸥žĚâÄżĄżŇŃÖŞĄ÷AĄäBĄäCĄäĘÇÓÉĄ÷ABCžšýĆ˝Ňƾþ˝ľÄŁŹËüĂǸ÷śĽľăÔÚĆ˝ĂćÖą˝Ç×řąęĎľÖĐľÄ×řąęČçĎÂąíËůĘžŁş
Ą÷ABC | AŁ¨aŁŹ0ŁŠ | BŁ¨3ŁŹ0ŁŠ | CŁ¨5ŁŹ5ŁŠ |
Ą÷AĄäBĄäCĄä | AĄäŁ¨4ŁŹ2ŁŠ | BĄäŁ¨7ŁŹbŁŠ | CĄäŁ¨cŁŹ7ŁŠ |
Ł¨1ŁŠšŰ˛ěąíÖи÷śÔÓŚľă×řąęľÄąäťŻŁŹ˛˘ĚîżŐŁşa=________ŁŹb=________ŁŹc=________Łť
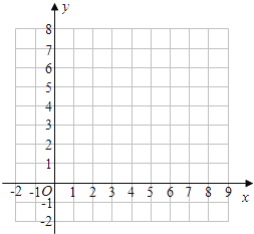
Ł¨2ŁŠÔÚĆ˝ĂćÖą˝Ç×řąęĎľÖĐťłöĄ÷ABCź°Ć˝ŇĆşóľÄĄ÷AĄäBĄäCĄäŁť
Ł¨3ŁŠÖą˝ÓĐ´łöĄ÷AĄäBĄäCĄäľÄĂćťýĘÇ________ŁŽ

