Question

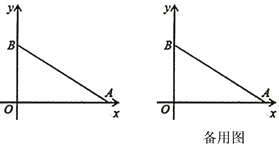
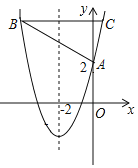
【题目】如图，已知二次函数y=ax2+bx+c的图象与x轴相交于A（﹣1，0），B（3，0）两点，与y轴相交于点C（0，﹣3）．

（1）求这个二次函数的表达式；

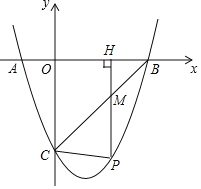
（2）若P是第四象限内这个二次函数的图象上任意一点，PH⊥x轴于点H，与BC交于点M，连接PC．

①求线段PM的最大值；

②当△PCM是以PM为一腰的等腰三角形时，求点P的坐标．

Answer 1

【答案】（1）二次函数的表达式y=x2﹣2x﹣3；（2）①PM最大=；②P（1，﹣4）或（，﹣2﹣1）．

【解析】（1）根据待定系数法，可得答案；

（2）①根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案；

②根据等腰三角形的定义，可得方程，根据解方程，可得答案．

（1）将A，B，C代入函数解析式，

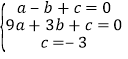得，解得，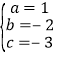

这个二次函数的表达式y=x2﹣2x﹣3；

（2）设BC的解析式为y=kx+b，

将B，C的坐标代入函数解析式，得

，解得，

BC的解析式为y=x﹣3，

设M（n，n﹣3），P（n，n2﹣2n﹣3），

PM=（n﹣3）﹣（n2﹣2n﹣3）=﹣n2+3n=﹣（n﹣）2+，

当n=时，PM最大=；

②当PM=PC时，（﹣n2+3n）2=n2+（n2﹣2n﹣3+3）2，

解得n1=0（不符合题意，舍），n2=2，

n2﹣2n﹣3=-3，

P（2，-3）；

当PM=MC时，（﹣n2+3n）2=n2+（n﹣3+3）2，

解得n1=0（不符合题意，舍），n2=3+（不符合题意，舍），n3=3-，

n2﹣2n﹣3=2-4，

P（3-，2-4）；

综上所述：P（2，﹣3）或（3-，2﹣4）．