Question

【题目】在数学学习中整体思想与转化思想是我们常用到的数学思想．

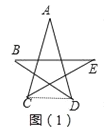
图(1)中，求∠A+∠B+∠C+∠D+∠E的度数等于多少时，我们可以连接CD，利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC，这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中，即∠A+∠B+∠C+∠D+∠E=_____.

图(2)中∠A+∠B+∠C+∠D+∠E的度数等于______.

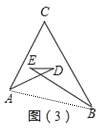
图(3)中∠A+∠B+∠C+∠D+∠E的度数等于________.

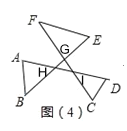
图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于________.

Answer 1

【答案】180°；180°；180°；360°．

【解析】

图（1）中，连接CD，可得∠B+∠E=∠ECD+∠BDC，故∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠ACD+∠ADC=180°；

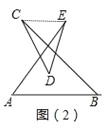
图（2）中，连接CE，可得∠A＋∠B＝∠AEC＋∠BCE，故∠A＋∠B＋∠DCB＋∠D＋∠DEA＝∠D+∠DCE+∠DEC＝180°；

图（3）中，连接AB，可得∠E＋∠D＝∠DAB+∠EBA，故∠CAD+∠CBE+∠C+∠D+∠E＝∠C+∠CAB+∠CBA＝180°；

图（4）中，可得∠A＋∠B＝∠HGI＋∠HIG，∠C＋∠D＝∠IHG+∠IGH，∠E＋∠F＝∠GHI+∠GIH，故∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝2（∠HGI+∠HIG+∠IHG）＝360°.

解：图（1）中，连接CD，

∵∠B+∠E=∠ECD+∠BDC，

∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠ACD+∠ADC=180°；

图（2）中，连接CE，

则∠A＋∠B＝∠AEC＋∠BCE，

∴∠A＋∠B＋∠DCB＋∠D＋∠DEA＝∠D+∠DCE+∠DEC＝180°；

图（3）中，连接AB，

则∠E＋∠D＝∠DAB+∠EBA，

∴∠CAD+∠CBE+∠C+∠D+∠E＝∠C+∠CAB+∠CBA＝180°；

图（4）中，∠A＋∠B＝∠HGI＋∠HIG，∠C＋∠D＝∠IHG+∠IGH，∠E＋∠F＝∠GHI+∠GIH，

∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝∠HGI＋∠HIG+∠IHG+∠IGH+∠GHI+∠GIH＝2（∠HGI+∠HIG+∠IHG）＝360°.

故答案为：180°；180°；180°；360°．