题目内容
【题目】九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 16 |
|
戏剧 | 4 | |
散文 | a |
|
其他 | b | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)直接写出a,b,m的值;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用列表法或画树状图的方法,求选取的2人恰好乙和丙的概率.

【答案】(1)a=8,b=12,m=30;(2)选取的2人恰好乙和丙的概率为![]() .
.
【解析】(1)先根据戏剧的人数及其所占百分比可得总人数,再用总人数乘以散文的百分比求得其人数,根据各类别人数之和等于总人数求得其他类别的人数,最后用其他人数除以总人数求得m的值;
(2)画树状图得出所有等可能的情况数,找出恰好是丙与乙的情况,即可确定出所求概率.
(1)∵被调查的学生总人数为4÷10%=40人,
∴散文的人数a=40×20%=8,其他的人数b=40﹣(16+4+8)=12,
则其他人数所占百分比m%=![]() ×100%=30%,即m=30;
×100%=30%,即m=30;
(2)画树状图,如图所示:
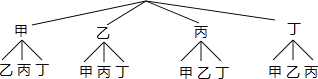
所有等可能的情况有12种,其中恰好是丙与乙的情况有2种,
所以选取的2人恰好乙和丙的概率为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目