题目内容
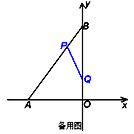
【题目】如图,在平面直角坐标系中,0为坐标原点,A、B两点的坐标分别为A(m,0)、B(0,n),且|m-n-3|+![]() =0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P运动时间为t秒.
=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P运动时间为t秒.
(1) 求OA、OB的长.
(2) 连接PB,若△POB的面积为3,求t的值.
(3) 过P作直线AB的垂线,垂足为D,直线PD与y轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.
【答案】(1)OA=6,OB=3;(2)若△POB的面积为3,则t的值为4或8;(3)存在这样的点P,使△EOP≌△AOB,t的值是3或9.
【解析】
(1)根据非负数的性质列方程求解即可;
(2)分两种情况:①当点P在线段AO上时,②当点P在线段AO的延长线上时,分别根据△POB的面积为3构造方程求解即可;
(3)当OP=OB=3时,分两种情况,画出符合条件的两种图形,可通过AAS证明两三角形全等,结合图形和全等三角形的性质即可得出答案.
解:(1)∵![]() ,
,
∴m-n-3=0,2n-6=0,
解得:n=3,m=6,
∴OA=6,OB=3;
(2)分两种情况:
①当点P在线段AO上时,
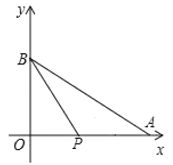
∵AP=t,
∴PO=6-t,
∴△POB的面积=![]() ,
,
解得:t=4;
②当点P在线段AO的延长线上时,
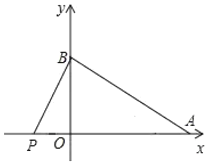
∵AP=t,
∴PO=t-6,
∴△POB的面积=![]() ,
,
解得:t=8,
综上,若△POB的面积为3,则t的值为4或8;
(3)当OP=OB=3时,分两种情况:
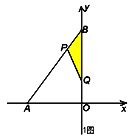
①如图:
∵∠BAO+∠APD=90°,∠APD=∠OPE,∠OPE+∠PEO=90°,
∴∠BAO=∠PEO,
又∵∠BOA=∠POE=90°,OP=OB,
∴△EOP≌△AOB(AAS),
∵OP=OB=3,
∴AP=6-3=3,
∴t=3,

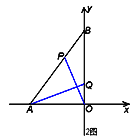
②如图:同理可证△EOP≌△AOB(AAS),
∵OP=OB=3,
∴AP=6+3=9,
∴t=9,

即存在这样的点P,使△EOP≌△AOB,t的值是3或9.