��Ŀ����
����Ŀ���ڡ�ABC�У�AB=AC����F��BC�ӳ�����һ�㣬��CFΪ�ߣ�������CDEF��ʹ����CDEF���A��BC��ͬ�࣬����BE����G��BE���е㣬����AG��DG��
��1����ͼ�٣�����BAC=��DCF=90��ʱ��ֱ��д��AG��DG��λ�ú�������ϵ��
��2����ͼ�ڣ�����BAC=��DCF=60��ʱ����̽��AG��DG��λ�ú�������ϵ��
��3������BAC=��DCF=��ʱ��ֱ��д��AG��DG��������ϵ��
���𰸡�
��1��
�⣺AG��DG��AG=DG��
֤�����ӳ�DG��BC����H������AH��AD��
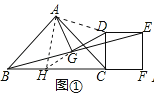
���ı���DCEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
�ڡ�BGH�͡�EGD��
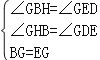
���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣬
�ߡ�DCF=90�㣬
���DCB=90�㣬
���ACD=45�㣬
���ABH=��ACD=45�㣬
�ڡ�ABH�͡�ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
�ߡ�BAH+��HAC=90�㣬
���CAD+��HAC=90�㣬����HAD=90�㣬
��AG��GD��AG=GD��
��2��
�⣺AG��GD��AG=![]() DG��
DG��
֤�����ӳ�DG��BC����H������AH��AD��

���ı���DCEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
�ڡ�BGH�͡�EGD��

���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=��DCF=60��
���ABC=60�㣬��ACD=60�㣬
���ABC=��ACD=60�㣬
�ڡ�ABH�͡�ACD��

���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
���BAC=��HAD=60�㣻
��AG��HD����HAG=��DAG=30�㣬
��tan��DAG=tan30��=![]() =
=![]() ��
��
��AG=![]() DG��
DG��
��3��
�⣺DG=AGtan![]() ��
��
֤�����ӳ�DG��BC����H������AH��AD��

���ı���DCEF�������Σ�
��DE=DC��DE��CF��
���GBH=��GED����GHB=��GDE��
��G��BC���е㣬
��BG=EG��
�ڡ�BGH�͡�EGD��
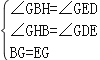
���BGH�ա�EGD��AAS����
��BH=ED��HG=DG��
��BH=DC��
��AB=AC����BAC=��DCF=����
���ABC=90�㩁![]() ����ACD=90�㩁
����ACD=90�㩁![]() ��
��
���ABC=��ACD��
�ڡ�ABH�͡�ACD��
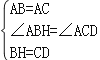
���ABH�ա�ACD��SAS����
���BAH=��CAD��AH=AD��
���BAC=��HAD=����
��AG��HD����HAG=��DAG=![]() ��
��
��tan��DAG=tan![]() =
=![]() ��
��
��DG=AGtan![]() ��
��
����������1���ӳ�DG��BC����H������AH��AD��ͨ��֤�á�BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤�á�ABH�ա�ACD���ó���BAH=��CAD��AH=AD��������á�HAD=90�㣬�������AG��GD��AG=GD��
��2���ӳ�DG��BC����H������AH��AD��ͨ��֤�á�BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤�á�ABH�ա�ACD���ó���BAH=��CAD��AH=AD��������á�HAD�ǵȱ������Σ�����֤��AG��GD��AG=![]() DG��
DG��
��3���ӳ�DG��BC����H������AH��AD��ͨ��֤�á�BGH�ա�EGD���BH=ED��HG=DG���ó�BH=DC��Ȼ��֤�á�ABH�ա�ACD���ó���BAH=��CAD��AH=AD��������á�HAD�ǵ��������Σ�����֤��DG=AGtan![]() ��
��
�����㾫����ͨ��������õ��������ε����ʺ����ε����ʣ����յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ������ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�뼴���Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij�̵깺��һ����Ʒ��ÿ����Ʒ����30Ԫ�������з���������Ʒÿ���������y��������ÿ�����ۼ�x��Ԫ���Ĺ�ϵ�������£�
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
��1����֪y��x����һ�κ�����ϵ�������ϱ������y��x֮��Ĺ�ϵʽ����д���Ա���x��ȡֵ��Χ����
��2������̵�����������Ʒ��ÿ��Ҫ���150Ԫ������ôÿ����Ʒ�����ۼ�Ӧ��Ϊ����Ԫ��
��3������̵�ÿ������������Ʒ��������Ϊw��Ԫ�������w��x֮��Ĺ�ϵʽ�������ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ�������





