题目内容
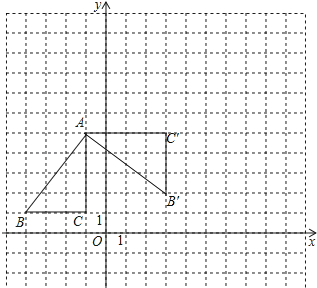
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C(﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,
(1)画出△AB′C′;
(2)写出点B′,C′的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
【答案】
(1)
解:△AB′C′如图所示;
(2)
解:点B′的坐标为(3,2),点C′的坐标为(3,5);
(3)
解:点C经过的路径为以点A为圆心,AC为半径的圆弧,路径长即为弧长,
∵AC=4,
∴弧长为:![]() =
=![]() =2π,
=2π,
即点C经过的路径长为2π.
【解析】(1)在平面直角坐标系中画出△ABC,然后根据网格结构找出点B、C的对应点B′,C′的位置,然后顺次连接即可;
(2)根据图形即可得出点A的坐标;
(3)利用AC的长,然后根据弧长公式进行计算即可求出点B转动到点B′所经过的路程.

练习册系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?