��Ŀ����
����Ŀ��ijУ�걨��������ɫ�˶���ѧУһ����������˲���ѧ���ġ�1�����������ɼ������Ƴ��������Ƶ���ֲ�ֱ��ͼ��ÿС�麬��Сֵ���������ֵ��������ͼ��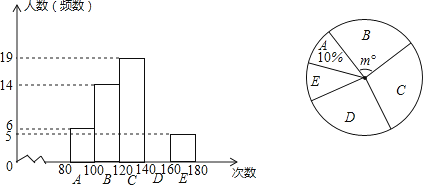
��1����ȫƵ���ֲ�ֱ��ͼ������ͼ��m=����
��2������ÿ���и����������������ݵ��м�ֵ���棨��A��80��x��100���м�ֵ��![]() =90�Σ�������ε��������ƽ�����Ƕ��٣�
=90�Σ�������ε��������ƽ�����Ƕ��٣�
��3�������1�����������ɼ����ڻ����120��Ϊ���㣬��ô��У2100��ѧ���С�1�����������ɼ�Ϊ����Ĵ�Լ�ж����ˣ�
���𰸡�
��1��
�⣺
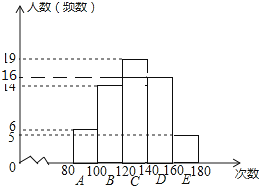
��ֱ��ͼ������ͼ��֪��A��������6�ˣ�ռ10%��
����������6��10%=60��
m=![]() ��360��=84�㣬
��360��=84�㣬
D��������60��6��14��19��5=16��
��2��
�⣺ƽ�����ǣ�![]() =130��
=130��
��3��
�⣺��Ϊ����Ĵ�Լ�У�2100��![]() =1400��
=1400��

����������1�������ɵڶ�С����10�ˣ�ռ20%����������������ٸ��ݸ�С��Ƶ��֮�͵�������������õ���С�������������ͳ��ͼ���������һС����ռ�ٷֱȣ��ٳ���360�㼴�������Ӧ����Բ�ĽǵĶ�����
��2�����ݼ�Ȩƽ�����ļ��㹫ʽ���ƽ�������ɣ�
��3����������гɼ������������ռ�İٷֱȣ��������������弴�ɣ�
���⿼����ͳ��ͼ��Ӧ�ã��漰֪ʶ�������������������壬����Բ�ĽǶ������Լ�ƽ������.