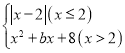题目内容
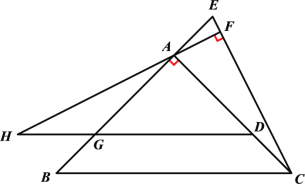
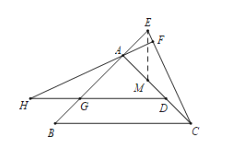
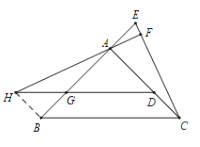
【题目】如图，△ABC中，AB=AC,∠BAC=90°,点D在AC上，点E在BA的延长线上，且CD=AE过点A作AF⊥CE,垂足为F,过点D作BC的平行线，交AB于点G,交FA的延长线于点H.
(1)求证∠ACE=∠BAH;
(2)在图中找出与CE相等的线段，并证明；
(3)若GH=
DH,求
的值（用含的代数式表示）.
【答案】（1）证明过程见解析;（2）与
相等的线段是
,证明过程见解析;（3）
.
【解析】
（1）根据
和
得到
和
，从而证明即可；
（2）在
上截取
，连接
，通过角度转换得到
证明AG=AD，从而证明
，即可证明AH=CE；
（3）连接
，先证
，得到
，从而证明四边形
是平行四边形，得到
，再证
设
，则
，从而得到
，即可求出.
（1）证明：
，
，
；
（2）与相等的线段是，证明如下：
在上截取，连接，
，
，
，
，
，
，
，
，
，
，
，
，
在△AGH和△CME中
，
；
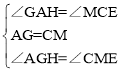
（3）解：连接，
∵，
∴AH=CE，
在△ABH和△CAE中
，
，
，
，
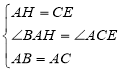
四边形是平行四边形，
，
，
设，则，
，
，
，
.
练习册系列答案
相关题目
