题目内容
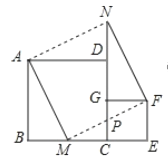
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M在BC边上,且BM=b,连接AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转至△NGF,给出以下五个结论:①∠MAD=∠AND;②△ABM≌△NGF;③CP=![]() ;④
;④![]() ;其中正确的个数是( )
;其中正确的个数是( )
A. 1B. 2C. 3D. 4
【答案】D
【解析】
①根据正方形的性质得到∠BAD=∠ADC=∠B=90°,根据旋转的性质得到∠NAD=∠BAM,∠AND=∠AMB,根据余角的性质得到∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,等量代换得到∠DAM=∠AND,故①正确;
②根据正方形的性质得到PC∥EF,根据相似三角形的性质得到CP=b-![]() ;故③正确;
;故③正确;
③根据旋转的性质得到GN=ME,等量代换得到AB=ME=NG,根据全等三角形的判定定理得到△ABM≌△NGF;故②正确;
④由旋转的性质得到AM=AN,NF=MF,根据全等三角形的性质得到AM=NF,推出四边形AMFN是矩形,根据余角的想知道的∠NAM=90°,推出四边形AMFN是正方形,于是得到S四边形AMFN=AM2=a2+b2;故④正确.
①∵四边形ABCD是正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAM+∠DAM=90°,
∵将△ABM绕点A旋转至△ADN,
∴∠NAD=∠BAM,∠AND=∠AMB,
∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,
∴∠DAM=∠AND,故①正确;
②∵四边形CEFG是正方形,
∴PC∥EF,
∴△MPC∽△EMF,
∴![]() ,
,
∵大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),BM=b,
∴EF=b,CM=a-b,ME=(a-b)+b=a,
∴![]() ,
,
∴CP=b-![]() ;故③正确;
;故③正确;
③∵将△MEF绕点F旋转至△NGF,
∴GN=ME,
∵AB=a,ME=a,
∴AB=ME=NG,
在△ABM与△NGF中,
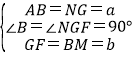 ,
,
∴△ABM≌△NGF;故②正确;
④∵将△ABM绕点A旋转至△ADN,
∴AM=AN,
∵将△MEF绕点F旋转至△NGF,
∴NF=MF,
∵△ABM≌△NGF,
∴AM=NF,
∴四边形AMFN是矩形,
∵∠BAM=∠NAD,
∴∠BAM+DAM=∠NAD+∠DAN=90°,
∴∠NAM=90°,
∴四边形AMFN是正方形,
∵在Rt△ABM中,a2+b2=AM2,
∴S四边形AMFN=AM2=a2+b2;故④正确.
故选D.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案