题目内容
【题目】如图,矩形OABC的项点A、C分别在![]() 、
、![]() 轴的正半轴上,点B点反比例函数
轴的正半轴上,点B点反比例函数![]() (k≠0)的第一象限内的图象上,OA=3,OC=5,动点P在
(k≠0)的第一象限内的图象上,OA=3,OC=5,动点P在![]() 轴的上方,且满足
轴的上方,且满足![]()
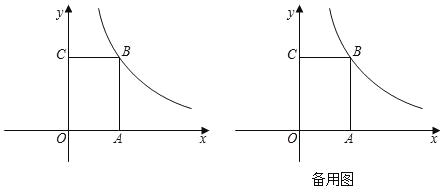
(1)若点P在这个反比例函数的图象上,求点P的坐标;
(2)连接PO、PA,求PO+PA的最小值;
(3)若点Q在平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标.
【答案】(1)P(5,3);(2)最小值为![]() ;(3)Q(
;(3)Q(![]() ,8)或(7,8)或(
,8)或(7,8)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)由矩形的性质可得出点B的坐标,利用反比例函数图象上点的坐标特征可求出k值,进而可得出反比例函数解析式,由![]() 可求出点P的纵坐标,再利用反比例函数图象上点的坐标特征可求出点P的坐标;
可求出点P的纵坐标,再利用反比例函数图象上点的坐标特征可求出点P的坐标;
(2)作点O关于直线y=3的对称点O′,连接AO′交直线y=3于点P,利用两点之间线段最短可得出此时PO+PA取得最小值,由点O的坐标可求出点O′的坐标,再利用勾股定理即可求出PO+PA的最小值;
(3)由线段AB的长及点P的纵坐标可得出AB只能为边,分点Q在点P的上方及点Q在点P的下方两种情况考虑:①当点Q在点P的上方时,由AP=AB=5可求出m的值,进而可得出点P1,P2的坐标,结合PQ=AB=5可得出点Q1,Q2的坐标;②当点Q在点P的下方时,由BP=AB=5可求出m的值,进而可得出点P3,P4的坐标,结合PQ=AB=5可得出点Q3,Q4的坐标.
(1)由题意,可知:点B的坐标为(3,5).
∵点B在反比例函数![]() (k≠0)的第一象限内的图象上,
(k≠0)的第一象限内的图象上,
∴k=3×5=15,
∴反比例函数的解析式为![]() ,
,
∵![]()
∴![]()
∴![]() .
.
当y=3时,![]() ,
,
解得:x=5,
∴当点P在这个反比例函数的图象上时,点P的坐标为(5,3).
(2)由(1)可知:点P在直线y=3上,作点O关于直线y=3的对称点O′,连接AO′交直线y=3于点P,此时PO+PA取得最小值,如图1所示.

∵点O的坐标为(0,0),
∴点O′的坐标为(0,6).
∵点A的坐标为(3,0),
∴AO′=![]() ,
,
∴PO+PA的最小值为![]() .
.
(3)∵AB∥y轴,AB=5,点P的纵坐标为3,
∴AB不能为对角线,只能为边.
设点P的坐标为(m,3),分两种情况考虑,如图2所示:

①当点Q在点P的上方时,AP=AB=5,即![]() ,
,
解得:m1=-1,m2=7,
∴点P1的坐标为(-1,3),点P2的坐标为(7,3).
又∵PQ=5,且PQ∥AB∥y轴,
∴点Q1的坐标为(-1,8),点Q2的坐标为(7,8);
②当点Q在点P的下方时,BP=AB=5,即![]() ,
,
解得:![]() ,
,![]() ,
,
同理,可得出:点Q3的坐标为(![]() ,-2),点Q4的坐标为(
,-2),点Q4的坐标为(![]() ,-2)
,-2)
综上所述:当以A、B、P、Q为顶点的四边形是菱形时,点Q的坐标为Q(![]() ,8)或(7,8)或(
,8)或(7,8)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)

 通城学典默写能手系列答案
通城学典默写能手系列答案【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;

(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).