题目内容
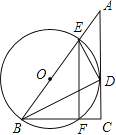
【题目】如图,AB是⊙O的直径,AD,BD是弦,点P在BA的延长线上,且
,延长PD交圆的切线BE于点E.
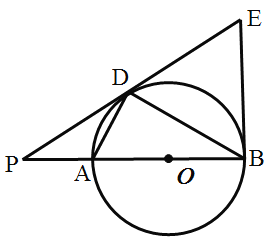
(1)求证:PD是⊙O的切线；
(2)若
,
,求PA的长.
【答案】（1） 详见解析；（2）1.
【解析】
（1）连接OD，如图1，利用等腰三角形的性质得∠1=∠OBD，加上∠PDA=∠PBD，则
，再根据圆周角定理得
，所以
，则根据切线的判定方法可判断PD为⊙O的切线；
（2）如图2，利用切线的性质得到
，
，设⊙O的半径为
，在Rt△PDO中，利用勾股定理进行计算，从而得到PA的长．
(1)证明:连接OD
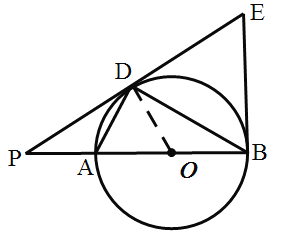
∵AB是⊙O的直径
∴
∴
∵
∴
∵
∴
∴
即PD⊥OD
∴直线PD为⊙O的切线；
(2)解:∵BE是⊙O的切线
∴
∵
∴
∵PD为⊙O的切线
∴
设⊙O的半径为
在Rt△PDO中,,则
∵
∴
解得
∴
,
∴
；
练习册系列答案
阅读快车系列答案
相关题目
