题目内容
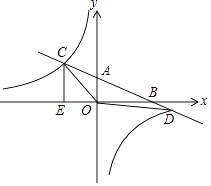
【题目】已知：抛物线的对称轴为x=﹣1，与x轴交于A，B两点，与y轴交于点C，其中A（﹣3，0）、C（0，﹣2）．
（1）求这条抛物线的函数表达式．
（2）已知在对称轴上存在一点P，使得△PBC的周长最小．请求出点P的坐标． 
（3）若点D是线段OC上的一个动点（不与点O、点C重合）．过点D作DE∥PC交x轴于点E．连接PD、PE．设CD的长为m，△PDE的面积为S．求S与m之间的函数关系式．试说明S是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．
【答案】
（1）解：设y=ax2+bx+c（a≠0），则
，
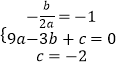解得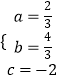 
，
∴此抛物线的解析式为y= 
x2+ 
x﹣2；
（2）解：如图，连接AC、BC．
因为BC的长度一定，所以△PBC周长最小，就是使PC+PB最小．
B点关于对称轴的对称点是A点，AC与对称轴x=﹣1的交点即为所求的点P．
设直线AC的表达式为y=kx+b，则
，
解得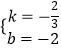 
，
∴此直线的表达式为y=﹣ x﹣2，
把x=﹣1代入得y=﹣
∴P点的坐标为（﹣1，﹣ ）；
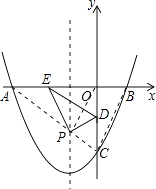
（3）解：S存在最大值，
理由：如图，∵DE∥PC，即DE∥AC，
∴△OED∽△OAC，
∴ 
= 
，即 
= 
，
∴OE=3﹣ 
m，OA=3，AE= m，
∴S=S△OAC﹣S△OED﹣S△AEP﹣S△PCD
= 
×3×2﹣ ×（3﹣ m）×（2﹣m）﹣ × m× ﹣ ×m×1
=﹣ 
m2+ m
=﹣ （m﹣1）2+
∵﹣ ＜0，
∴当m=1时，S最大= ．
【解析】（1）已知抛物线过C（0，﹣2）点，那么c=﹣2；根据对称轴为x=﹣1，因此﹣ 
=﹣1，然后将A点的坐标代入抛物线中，通过联立方程组即可得出抛物线的解析式；（2）本题的关键是确定P点的位置，由于A是B点关于抛物线对称轴的对称点，因此连接AC与抛物线对称轴的交点就是P点．可根据A，C的坐标求出AC所在直线的解析式，然后根据一次函数的解析式求出与抛物线对称轴的交点，即可得出P点的坐标；（3）△PDE的面积=△OAC的面积﹣△PDC的面积﹣△ODE的面积﹣△AEP的面积，△OAC中已知A，C的坐标，可求出△OAC的面积．△PDC中以CD为底边，P的横坐标的绝对值为高，即可表示出△PDC的面积．△ODE中可先用m表示出OD的长，然后根据△ODE与△OAC相似，求出OE的长，根据三角形的面积计算公式可用m表示出△ODE的面积．△PEA中以AE为底边（可用OE的长表示出AE），P点的纵坐标的绝对值为高，可表示出△PEA的面积．由此可表示出△ODE的面积，即可得出关于S，m的函数关系式．然后根据函数的性质，求出三角形的最大面积以及对应的m的值．
【考点精析】通过灵活运用确定一次函数的表达式和相似三角形的判定与性质，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．
