题目内容
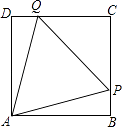
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( ) 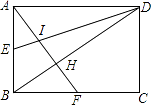
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:延长AF交DC于Q点,如图所示: ∵E,F分别是AB,BC的中点,
∴AE= ![]() AB=3,BF=CF=
AB=3,BF=CF= ![]() BC=4,
BC=4,
∵四边形ABCD是矩形,
∴CD=AB=6,AB∥CD,AD∥BC,
∴ ![]() =1,△AEI∽△QDE,
=1,△AEI∽△QDE,
∴CQ=AB=CD=6,△AEI的面积:△QDI的面积=3:12=1:4,
∵AD=8,
∴△AEI中AE边上的高= ![]() ,
,
∴△AEI的面积= ![]() ×3×
×3× ![]() =
= ![]() ,
,
∵△ABF的面积= ![]() ×4×6=12,
×4×6=12,
∵AD∥BC,
∴△BFH∽△DAH,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴△BFH的面积= ![]() ×2×4=4,
×2×4=4,
∴四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积=12﹣ ![]() ﹣4=
﹣4= ![]() .
.
故选:C.
延长AF交DC于Q点,由矩形的性质得出CD=AB=6,AB∥CD,AD∥BC,得出 ![]() =1,△AEI∽△QDE,因此CQ=AB=CD=6,△AEI的面积:△QDI的面积=3:12=1:4,∵AD=8,求出△AEI的面积=
=1,△AEI∽△QDE,因此CQ=AB=CD=6,△AEI的面积:△QDI的面积=3:12=1:4,∵AD=8,求出△AEI的面积= ![]() ,△ABF的面积=12,△BFH的面积=4,四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积,即可得出结果.
,△ABF的面积=12,△BFH的面积=4,四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积,即可得出结果.

练习册系列答案
相关题目