题目内容
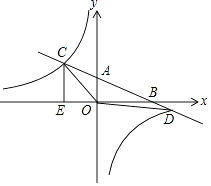
【题目】直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2. 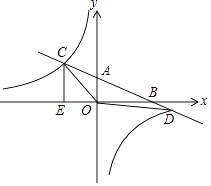
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积.
【答案】
(1)解:在Rt△AOB中,∵tan∠ABO=0.5,OB=4,
∴OA=2,
∴A(0,2),B(4,0),设直线AB的解析式为y=kx+b,则有 ![]() ,解得
,解得 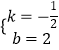 ,
,
∴直线AB的解析式为y=﹣ ![]() x+2,
x+2,
∵OE=2,CE⊥x轴,
∴C(﹣2,3),设反比例函数的解析式为y= ![]() ,
,
∴k=﹣6,
∴直线AB和反比例函数的解析式分别为y=﹣ ![]() x+2,y=﹣
x+2,y=﹣ ![]() .
.
(2)解:由 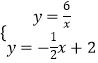 解得
解得 ![]() 或
或 ![]() ,
,
∴D(6,﹣1),
∴S△COD=S△AOC+S△AOD= ![]() ×2×2+
×2×2+ ![]() ×2×6=8.
×2×6=8.
【解析】(1)在Rt△AOB中,由tan∠ABO=0.5,OB=4,推出OA=2,推出A(0,2),B(4,0),设直线AB的解析式为y=kx+b,利用待定系数法即可解决问题.(2)利用方程组求出点D坐标,根据S△COD=S△AOC+S△AOD计算即可.
【考点精析】关于本题考查的解直角三角形,需要了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.

练习册系列答案
相关题目