Question

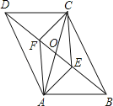
【题目】如图，在平行四边形ABCD中，已知AD＞AB．

（1）实践与操作：作∠BAD的平分线交BC于点E，在AD上截取AF=AB，连接EF；（要求：尺规作图，保留作图痕迹，不写作法）

（2）猜想并证明：猜想四边形ABEF的形状，并给予证明．

Answer 1

【答案】（1）作图见解析；（2）证明见解析.

【解析】（1）由角平分线的作法容易得出结果，在AD上截取AF=AB，连接EF；画出图形即可；（2）由平行四边形的性质和角平分线得出∠BAE=∠AEB，证出BE=AB，由（1）得：AF=AB，得出BE=AF，即可得出结论．

解：（1）如图AE就是所要求的角平分线。

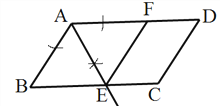
（2）四边形ABEF是菱形；理由如下：

∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠DAE=∠AEB，

∵AE平分∠BAD，

∴∠BAE=∠DAE，

∴∠BAE=∠AEB，∴BE=AB，

由（1）得：AF=AB，

∴BE=AF，又∵BE∥AF，

∴四边形ABEF是平行四边形，

∵AF=AB，

∴四边形ABEF是菱形．