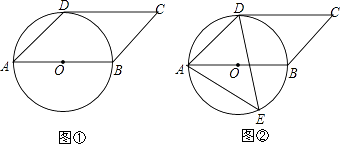
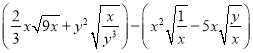题目内容
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c)
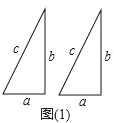
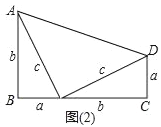
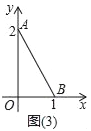
(1)用这样的两个三角形构造成如图(2)的图形,利用这个图形,证明:a2+b2=c2;
(2)用这样的两个三角形可以拼出多种四边形,画出周长最大的四边形;当a=2,b=4时,求这个四边形的周长;
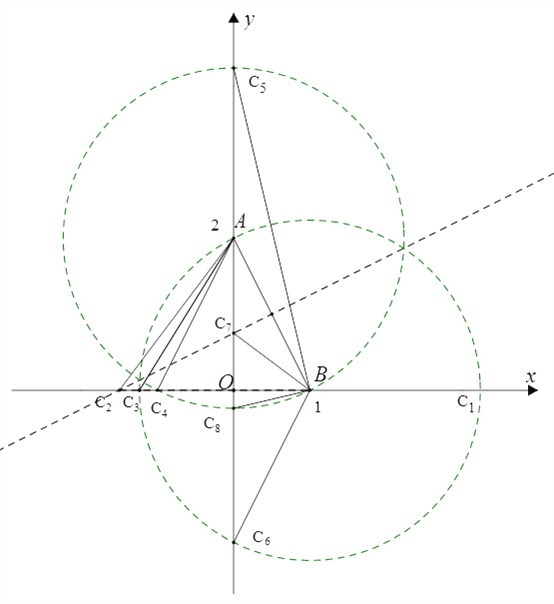
(3)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
①请在x轴、y轴上找一点C,使△ABC为等腰三角形;(要求:用尺规画出所有符合条件的点,并用C1,C2,…,Cn在图中标出所找的点.只保留作图痕迹,不写作法)
②写出一个满足条件的在x轴上的点的坐标:_____,写出一个满足条件的在y轴上的点坐标:_____.
【答案】(1)证明见解析;(2)画图见解析,周长为![]() ;(3)①作图见解析;②(
;(3)①作图见解析;②( ![]() ,0),(0,
,0),(0, ![]() )(答案不唯一).
)(答案不唯一).
【解析】试题分析:(1)由图知,梯形的面积等于三个直角三角形的面积之和,用字母表示出来,化简后,即证明勾股定理;
(2)由a与b的值,利用勾股定理求出c的值,拼图后可知如图1所示时周长最大,求出最大周长即可;
(3)①分别以A、B为圆心,AB长为半径画圆,圆与坐标轴的交点即为满足条件的点,再作线段AB的垂直平分线,垂直平分线与坐标轴的交点也是满足条件的点;
②根据①所作的图形即可得.
试题解析:(1)由图可得, ![]() ×(a+b)(a+b)=
×(a+b)(a+b)=![]() ab+
ab+![]() c2+
c2+![]() ab,
ab,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2;
(2)当a=2,b=4时,可得:c=![]() ,
,
如图1时:四边形的周长为:8+4![]() ;
;
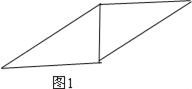
如图2时,四边形的周长为:12;
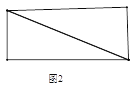
如图3时,四边形的周长为:4+4![]() ;
;

综上,图1是周长最大的四边形,周长为:8+4![]() ;
;
(3)①如图所示;
②如上图:
一个满足条件的在x轴上的点的坐标:如C3(﹣1,0);
一个满足条件的在y轴上的点的坐标:如C5(0,2+![]() ).
).
故答案为:(﹣1,0);(0,2+![]() )(答案不唯一).
)(答案不唯一).

【题目】“元旦”期间,某文具店购进100只两种型号的文具进行销售,其进价和售价如下
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)该店用1300元可以购进A,B两种型号的文具各多少只?
(2)若把所购进A,B两种型号的文具全部销售完,利润率超过40%没有?请你说明理由.