题目内容
21、如图，已知平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F两点，垂足是点O．（1）求证：△AOE≌△COF；
（2）问：四边形AFCE是什么特殊的四边形？（直接写出结论，不需要证明）．
分析：（1）根据平行四边形ABCD的对边相互平行知，AD∥BC；然后由两直线平行，内错角相等，得∠EAO=∠FCO，∠AEO=∠CFO；最后根据全等三角形的判定定理ASA来证明△AOE≌△COF；
（2）菱形的对角线互相垂直平分．
（2）菱形的对角线互相垂直平分．
解答：（1）证明：∵四边形ABCD是平行四边形，
∴AD∥BC（平行四边形的对边相互平行）．
∴∠EAO=∠FCO，∠AEO=∠CFO（两直线平行，内错角相等）；
∵EF垂直平分AC，
∴OA=OC．
在△AOE和△COF中，
∠EAO=∠FCO，∠AEO=∠CFO，OA=OC．
∴△AOE≌△COF（ASA）；
（2）四边形AFCE是菱形．
∴AD∥BC（平行四边形的对边相互平行）．
∴∠EAO=∠FCO，∠AEO=∠CFO（两直线平行，内错角相等）；
∵EF垂直平分AC，
∴OA=OC．
在△AOE和△COF中，
∠EAO=∠FCO，∠AEO=∠CFO，OA=OC．
∴△AOE≌△COF（ASA）；
（2）四边形AFCE是菱形．
点评：本题主要考查了平行四边形的性质、菱形的判定、全等三角形的判定与性质．菱形的判别方法是说明一个四边形为菱形的理论依据，常用三种方法：
①定义；
②四边相等；
③对角线互相垂直平分．
①定义；
②四边相等；
③对角线互相垂直平分．
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．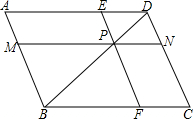
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．