题目内容
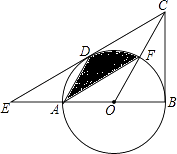
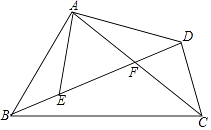
【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且 ![]() .
. 
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由.
【答案】
(1)解:∠BAE与∠CAD相等.
理由:∵ ![]() ,
,
∴△ABC∽△AED,
∴∠BAC=∠EAD,
∴∠BAE=∠CAD
(2)解:△ABE与△ACD相似.
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
在△ABE与△ACD中,
∵ ![]() =
= ![]() ,∠BAE=∠CAD,
,∠BAE=∠CAD,
∴△ABE∽△ACD
【解析】(1)先根据题意得出△ABC∽△AED,由相似三角形的性质即可得出结论;(2)先根据题意得出 ![]() =
= ![]() ,再由∠BAE=∠CAD即可得出结论.
,再由∠BAE=∠CAD即可得出结论.
【考点精析】通过灵活运用相似三角形的判定,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)即可以解答此题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目