题目内容
【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，且抛物线经过A（﹣1，0），C（0，﹣5）两点，与x轴交于点B．
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）设点P为抛物线上的一个动点，连接PB、PC，若△BPC是以BC为直角边的直角三角形，求此时点P的坐标；
（3）在抛物线上BC段有另一个动点Q，以点Q为圆心作⊙Q，使得⊙Q与直线BC相切，在运动的过程中是否存在一个最大⊙Q？若存在，请直接写出最大⊙Q的半径；若不存在，请说明理由．
【答案】
（1）
解：∵对称轴为x=2，且抛物线经过A（﹣1，0），
∴B（5，0）．
把B（5，0），C（0，﹣5）分别代入y=mx+n得 
，解得： 
，
∴直线BC的解析式为y=x﹣5．
设y=a（x﹣5）（x+1），把点C的坐标代入得：﹣5a=﹣5，解得：a=1，
∴抛物线的解析式为：y=x2﹣4x﹣5
（2）
解：①过点C作CP1⊥BC，交抛物线于点P1，如图，
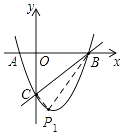
则直线CP1的解析式为y=﹣x﹣5，
由 
，解得： 
（舍去）， 
，
∴P1（3，﹣8）；
②过点B作BP2⊥BC，交抛物线于P2，如图，
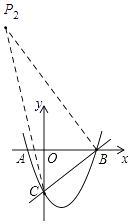
则BP2的解析式为y=﹣x+5，
由 ，解得： 
（舍去）， 
，
∴P2（﹣2，7）
（3）
解：由题意可知，Q点距离BC最远时，半径最大．平移直线BC，使其与抛物线只有一个公共点Q（即相切），设平移后的直线解析式为y=x+t，
由 
，消去y整理得x2﹣5x﹣5﹣t=0，
△=25+4（5+t）=0，解得t=﹣ 
，
∴平移后与抛物线相切时的直线解析式为y=x﹣ ，且Q（ 
，﹣ 
），
连接QC、QB，作QE⊥BC于E，如图，
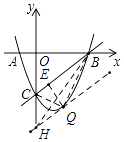
设直线y=x﹣ 与y轴的交点为H，连接HB，
则 
，
∵CH=﹣5﹣（﹣ ）= 
，
∴ 
= 
，
∴ 
，
∵ 
，BC= 
，
∴QE= 
，
即最大半径为
【解析】（1）根据对称轴及A点坐标得出B点坐标，从而得出直线BC解析式，再由A、B、C三点坐标得出抛物线解析式；（2）分别过B、C两点作BC的垂线，得出垂线的解析式，与抛物线解析式联立解出P点；（3）平移BC到与抛物线刚好相切之处，此时的切点即为Q点，此时Q点距BC的距离最大，也就是半径最大．由于初中阶估没学点到直线的距离公式，那么这里可以用等面积法进行处理．设切线与y轴的交点为H，则△HBC与△QBC的面积相等，算出面积，再以BC为底，算出BC边上的高即为答案．
