题目内容
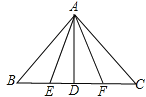
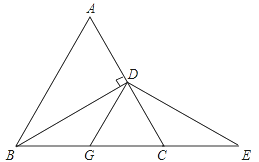
【题目】如图所示,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,DG∥AB,DG交BC于点G,点E在BC的延长线上,且CE=CD.
(1)求∠ABD和∠BDE的度数;
(2)写出图中的等腰三角形(写出3个即可).
【答案】(1) ∠CDE=30° ∠BDE=120° (2) △ABC是等腰三角形 ,△CDG为等腰三角形,△CDE是等腰三角形
【解析】
(1)△ABC是等边三角形,所以△ABD是直角三角形,可求∠ABD,再利用线段相等,角的转化,求出∠BDE;
(2)只要两边相等或者两个角相等,就是等腰三角形,在图形中找相等的角即可.
(1)∵AB=AC,∠A=60°,
∴△ABC是等边三角形,
∵BD⊥AC,
∴∠ABD=30°,
∵CD=CE,∠ACB=60°
∴∠CDE=30°
∴∠BDE=120°.
(2)∵AB=AC,
∴△ABC是等腰三角形
∵DG∥AB,
∴∠DGC=∠ABC,
∴△CDG为等腰三角形.
∵CD=CE,
∴△CDE是等腰三角形.

练习册系列答案
相关题目
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.