题目内容
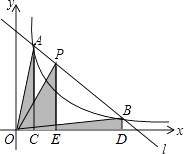
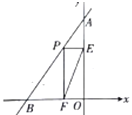
【题目】如图,直线AB的解析式为y=![]() x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
【答案】![]()
【解析】
在一次函数y=![]() x+4中,分别令x=0, y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,根据直角三角形面积的不同表示方法可求得OP的长,即可求得EF的最小值.
x+4中,分别令x=0, y=0,解相应方程,可求得A、B两点的坐标,由矩形的性质可知EF=OP,可知当OP最小时,则EF有最小值,由垂线段最短可知当OP⊥AB时,满足条件,根据直角三角形面积的不同表示方法可求得OP的长,即可求得EF的最小值.
∵一次函数y=![]() x+4中,令x=0,则y=4,令y=0,则x=-3,
x+4中,令x=0,则y=4,令y=0,则x=-3,
∴A(0,4),B(-3,0),
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵A(0,4),点B坐标为(-3,0),
∴OA=4,OB=3,
由勾股定理得:AB=![]() =5,
=5,
∵AB·OP=AO·BO=2S△OAB,
∴OP=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目