题目内容
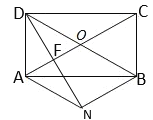
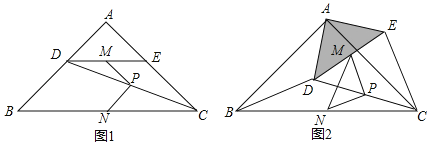
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() 点
点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动时,另一个点也停止运动.连接
;当一个点停止运动时,另一个点也停止运动.连接![]() ,过点
,过点![]() 作
作![]() ,设运动时间为
,设运动时间为![]() ,
,
解答下列问题:
(1)当![]() 为何值时
为何值时![]() 是等腰三角形?
是等腰三角形?
(2)设五边形![]() 面积为
面积为![]() ,试确定
,试确定![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻![]() 使得
使得![]() 平分
平分![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
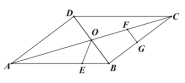
【答案】(1)![]() 或
或![]() 或
或![]() (2)
(2)![]() (3)存在;
(3)存在;![]() (4)存在;
(4)存在;![]()
【解析】
(1)分三种情况:![]() ,
,![]() ,
,![]() 分类讨论即可;
分类讨论即可;
(2)过点![]() 作
作![]() 于点
于点![]() ,先求出
,先求出![]() 的面积,再求出四边形
的面积,再求出四边形![]() 的面积,把两个面积相加即可;
的面积,把两个面积相加即可;
(3)过点![]() 作
作![]() 于点
于点![]() ,求出
,求出![]() ,再求出
,再求出![]() 的面积,由第二问我们可以知道五边形
的面积,由第二问我们可以知道五边形![]() 面积表达式,根据
面积表达式,根据![]() 列出方程即可得出答案;
列出方程即可得出答案;
(4)过点![]() 作
作![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,利用
,利用![]() ,得出
,得出![]() ,设
,设![]() ,则
,则![]() ,利用
,利用![]() ,得出
,得出![]() 的表达式,在
的表达式,在![]() 中,利用勾股定理列出方程,求出
中,利用勾股定理列出方程,求出![]() ,进而求出
,进而求出![]() ,从而得出答案.
,从而得出答案.
解:∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 都是直角三角形,
都是直角三角形,
∴![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
(1)当![]() ,
,
由题意知道:![]() ,∴
,∴![]() ,即
,即![]() ;
;
当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即:
,即: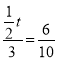 ,
,
解得:![]() ;
;
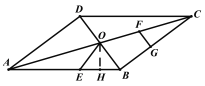
当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ;
;
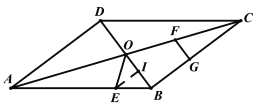
综上所述:当![]() 、
、![]() 或
或![]() 时,
时,![]() 是等腰三角形;
是等腰三角形;
(2)过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴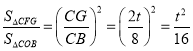 ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ;
;
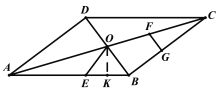
(3)存在;
理由如下:
过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴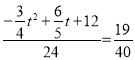 ,
,
整理得:![]()
解得:![]() ,
,
∵![]() 不能为负数,
不能为负数,
∴![]() 舍去,
舍去,
∴![]() ,
,
∴当![]() 时,
时,![]() ;
;
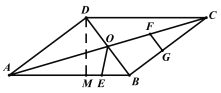
(4)存在;
理由如下:
过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,即
,即![]() ,
,
整理得:![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∵![]() 不能为负数,∴
不能为负数,∴![]() 舍去,
舍去,
∴![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 平分
平分![]() .
.

【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
250 | |
x |
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
【题目】为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= .n= ;
(3)补全频数分布直方图:
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在 分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是