题目内容
【题目】为了解2012年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |

请根据以上图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= .n= ;
(3)补全频数分布直方图:
(4)参加比赛的小聪说,他的比赛成绩是所有抽查同学成绩的中位数,据此推断他的成绩落在 分数段内;
(5)如果比赛成绩80分以上(含80分)为优秀,那么你估计该竞赛项目的优秀率大约是
【答案】(1)300;(2)120;0.3;(3)答案见解析;(4)80≤x<90;(5)60%
【解析】
(1)利用第一组的频数除以频率即可得到样本容量:30÷0.1=300.
(2)m=0.4×300=120,n=90÷300=0.3.
(3)根据80≤x<90组频数即可补全直方图.
(4)根据中位数定义,找到位于中间位置的两个数所在的组即可:中位数为第150个数据和第151个数据的平均数,而第150个数据和第151个数据位于80≤x<90这一组,故中位数位于80≤x<90这一组.
(5)将比赛成绩80分以上的两组数的频率相加即可得到计该竞赛项目的优秀率.
解:(1)此次调查的样本容量为30÷0.1=300;
故答案为:300;
(2)n=![]() =0.3;m=0.4×300=120;
=0.3;m=0.4×300=120;
故答案为:120;0.3;
(3)补全频数分布直方图如图:
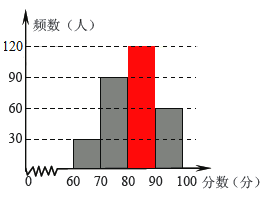
(4)中位数为第150个数据和第151个数据的平均数,而第150个数据和第151个数据位于80≤x<90这一组,故中位数位于80≤x<90这一组;
故答案为:80≤x<90
(5)将80≤x<90和90≤x≤100这两组的频率相加即可得到优秀率,优秀率为60%.
故答案为:60%.

 名校课堂系列答案
名校课堂系列答案【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?