题目内容
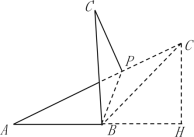
【题目】已知:如图,∠ABC=135°,AB=a,BC=b,点P是边AC上任意一点,连结BP,将△CPB沿PB翻折,得△C'PB.
(1)若a=![]() ,b=6,∠C'PC=90°,求CP的长;
,b=6,∠C'PC=90°,求CP的长;
(2)连结AC',当以A、B、P、C'为顶点的四边形是平行四边形时,求![]() 的值.
的值.
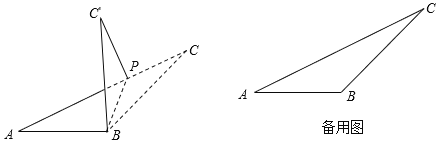
【答案】(1)![]() (2)
(2)![]() 或
或![]()
【解析】
(1)本题以三角形为背景,考查“翻折图形”性质以及相似三角形的判定,根据特殊角度135°,可利用辅助线构造45°,结合垂直构造等腰直角三角形,进而推出边等进行计算.
(2)本题考查平行四边形性质以及翻折图形性质、需根据动点位置不同采取分类讨论方式,利用四边形性质求解.
(1)解:由翻折,∠CPB=∠C'PB
∵∠C'PC=90°
∴∠CPB=135°
又∵∠PCB=∠BCA,∠ABC=135°
∴△CPB∽△CBA
∴![]()
过点C作CH⊥AB交AB延长线于点H,如下图
∴∠CBH=45°
∴CH=BH=![]()
∴AH=![]()
在Rt△CAH中,CA=![]() =
=![]()
∴![]()
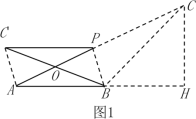
(2)①如图1,
∵四边形ABPC'是平行四边形以及翻折条件
∴∠C'BA=∠BCP=∠BC'P
∵∠OAB=∠BAC
∴△OAB∽△BAC,OB=![]()
∴![]()
过点C作CH⊥AB交AB延长线于点H
∴CH=BH=![]()
∴CA=![]() =
=![]()
∴![]()
∴![]() 或
或![]() (舍去)
(舍去)
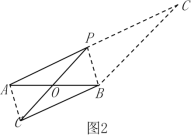
②如图2,
∵四边形APBC'是平行四边形
∴OA=OB
又∵翻折后得平行四边形PCBC'
∴AP=BC=PC
结合上一问所求AC值
∴![]()
∴![]() 或
或![]() (舍去)
(舍去)
∴综上,![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案【题目】新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1 |
录播 | 4 | 16 | 12 | 8 |
直播 | 2 | 10 | 16 | 12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0.4以下的共有多少人?
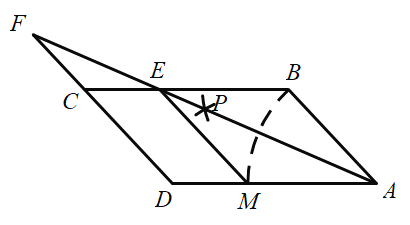
【题目】在![]() 中,
中,![]() ,
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()