题目内容
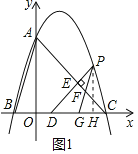
【题目】如图1,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+c与y轴交于点A(0,6),与x轴交于点B(﹣2,0),C(6,0).
(1)直接写出抛物线的解析式及其对称轴;
(2)如图2,连接AB,AC,设点P(m,n)是抛物线上位于第一象限内的一动点,且在对称轴右侧,过点P作PD⊥AC于点E,交x轴于点D,过点P作PG∥AB交AC于点F,交x轴于点G.设线段DG的长为d,求d与m的函数关系式,并注明m的取值范围;
(3)在(2)的条件下,若△PDG的面积为![]() ,
,
①求点P的坐标;
②设M为直线AP上一动点,连接OM交直线AC于点S,则点M在运动过程中,在抛物线上是否存在点R,使得△ARS为等腰直角三角形?若存在,请直接写出点M及其对应的点R的坐标;若不存在,请说明理由.

【答案】(1)y![]() (x﹣2)2+8,抛物线对称轴为直线x=2;(2)d=
(x﹣2)2+8,抛物线对称轴为直线x=2;(2)d=![]() m2
m2![]() m+4(2<m<6);(3)①点P坐标为(5,
m+4(2<m<6);(3)①点P坐标为(5,![]() ),②M1(
),②M1(![]() ,
,![]() ),R1(2,8);M2(
),R1(2,8);M2(![]() ,
,![]() ),R2(2,8);M3(
),R2(2,8);M3(![]() ,
,![]() ),R3(4,6);M4(6,3),R4(4,6).
),R3(4,6);M4(6,3),R4(4,6).
【解析】
(1)已知抛物线与x轴交点B、C,故可设交点式,再把点A代入即求得抛物线解析式.用配方法或公式求得对称轴.
(2)过点P作PH⊥x轴于点H,由PD⊥AD于点E易证∠PDH=45°,故DH=PH=n.由PG∥AB易证△PGH∽△ABO,利用对应边成比例可得GH![]() n,把含m的式子代入d=DH﹣GH即得到d与m的函数关系式,再由点P的位置确定2<m<6.
n,把含m的式子代入d=DH﹣GH即得到d与m的函数关系式,再由点P的位置确定2<m<6.
(3)①用n表示DG、PH,代入S△PDG![]() DGPH
DGPH![]() ,求得n的值(舍去负值),再利用n
,求得n的值(舍去负值),再利用n![]() m2+2m+6解关于m的方程即求得点P坐标.
m2+2m+6解关于m的方程即求得点P坐标.
②因为△ARS为等腰直角三角形且AS与y轴夹角为45°,故AR与y轴夹角为45°或90°.由于不确定△ARS哪个为直角顶点,故需分3种情况讨论,画出图形,利用45°或90°来确定点R、S的位置,进而求点R、S坐标,再由S的坐标求直线OM解析式,把直线OM与直线AP解析式联立方程组,解得点M坐标.
解:(1)∵抛物线与x轴交于点B(﹣2,0),C(6,0)
∴设交点式y=a(x+2)(x﹣6)
∵抛物线过点A(0,6)
∴﹣12a=6
∴a![]()
∴抛物线解析式为y![]() (x+2)(x﹣6)
(x+2)(x﹣6)![]() x2+2x+6
x2+2x+6![]() (x﹣2)2+8
(x﹣2)2+8
∴抛物线对称轴为直线x=2.
(2)过点P作PH⊥x轴于点H,如图1
∴∠PHD=90°
∵点P(m,n)是抛物线上位于第一象限内的一动点且在对称轴右侧
∴2<m<6,PH=n![]() m2+2m+6,n>0
m2+2m+6,n>0
∵OA=OC=6,∠AOC=90°
∴∠ACO=45°
∵PD⊥AC于点E
∴∠CED=90°
∴∠CDE=90°﹣∠ACO=45°
∴DH=PH=n
∵PG∥AB
∴∠PGH=∠ABO
∴△PGH∽△ABO
∴![]()
∴GH![]() n
n
∴d=DH﹣GH=n![]() n
n![]() n
n![]() (
(![]() m2+2m+6)
m2+2m+6)![]() m2
m2![]() m+4(2<m<6)
m+4(2<m<6)
(3)①∵S△PDG![]() DGPH
DGPH![]()
∴![]() nn
nn![]()
解得:n1![]() ,n2
,n2![]() (舍去)
(舍去)
∴![]() m2+2m+6
m2+2m+6![]()
解得:m1=﹣1(舍去),m2=5
∴点P坐标为(5,![]() )
)
②在抛物线上存在点R,使得△ARS为等腰直角三角形.
设直线AP解析式为y=kx+6
把点P代入得:5k+6![]()
∴k![]()
∴直线AP:y![]() x+6
x+6
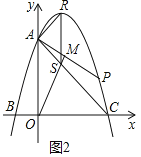
i)若∠RAS=90°,且S在线段AC上,如图2
∵直线AC解析式为y=﹣x+6
∴直线AR解析式为y=x+6
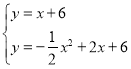 解得:
解得: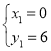 (即点A)
(即点A)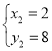
∴R(2,8)
∵∠ASR=∠OAC=45°
∴RS∥y轴
∴xS=xR=2
∴S(2,4)
∴直线OM:y=2x
∵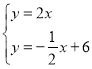 解得:
解得: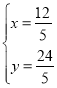
∴M(![]() ,
,![]() )
)
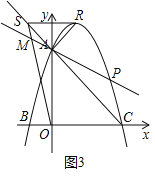
ii)若∠RAS=90°,且S在线段CA延长线上,如图3
∴R(2,8)
∴yS=yR=8
∴S(﹣2,8)
∴直线OM:y=﹣4x
∵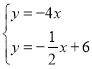 解得:
解得: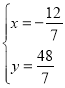
∴M(![]() ,
,![]() )
)
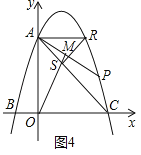
iii)若∠ASR=90°,如图4
∴∠SAR=∠ACO=45°
∴AR∥x轴
∴R(4,6)
∵S在AR的垂直平分线上
∴S(2,4)
∴M(![]() ,
,![]() )
)
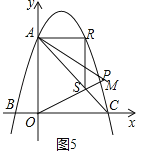
iiii)若∠ARS=90°,如图5
∴∠SAR=∠ACO=45°,RS∥y轴
∴AR∥x轴
∴R(4,6)
∴S(4,2)
∴直线OM:y![]() x
x
∵ 解得:
解得:![]()
∴M(6,3)
综上所述,M1(![]() ,
,![]() ),R1(2,8);M2(
),R1(2,8);M2(![]() ,
,![]() ),R2(2,8);M3(
),R2(2,8);M3(![]() ,
,![]() ),R3(4,6);M4(6,3),R4(4,6).
),R3(4,6);M4(6,3),R4(4,6).