��Ŀ����
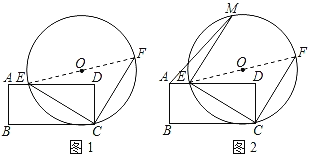
����Ŀ����ͼ1����E�ھ���ABCD�ı�AD�ϣ�AD��6��tan��ACD��![]() ������CE���߶�CE�Ƶ�C��ת90�㣬�õ��߶�CF�����߶�EFΪֱ������O��
������CE���߶�CE�Ƶ�C��ת90�㣬�õ��߶�CF�����߶�EFΪֱ������O��
��1����˵����Cһ������O�ϵ����ɣ�
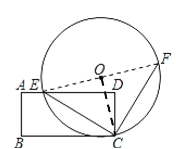
��2����M����O�ϣ���ͼ2��MCΪ��O��ֱ������֤����M��AD�ľ�������߶�DE�ij���
��3������AEM���ȡ�����ֵʱ������O�뾶�ij���
��4������O�����ABCD�ı�����ʱ����������OCF�������
���𰸡���1������������2��֤������������3��![]()
![]() ����4��4��
����4��4��
��������
��1������OC������ת�����ʵó���ECF��90�㣬��ֱ��������б�ߵ����ߵ����ʵó�OC��OE��OF�����ɵó���Cһ������O�ϣ�
��2����֤EM��CE������M��MN��AD��N����AAS֤�á�MEN�ա�CED���ó�MN��DE�����ɵó����ۣ�
��3����AE��x����DE��6��x���ɣ�2���õ�M��AD�ľ�������߶�DE�ij�����S��AEM��![]() ��x����6��x������
��x����6��x������![]() ��x��3��2+
��x��3��2+![]() ����x��3ʱ����AEM���ȡ�����ֵ
����x��3ʱ����AEM���ȡ�����ֵ![]() ����ʱ��DE��3����tan��ACD��
����ʱ��DE��3����tan��ACD��![]() ��
��![]() ���ó�CD��4���ɹ��ɶ�����CE2��DE2+CD2�����CE��5����֤��CEF��45�㣬��Rt��CEF�У���EF��
���ó�CD��4���ɹ��ɶ�����CE2��DE2+CD2�����CE��5����֤��CEF��45�㣬��Rt��CEF�У���EF��![]() �����ɵó������
�����ɵó������
��4������O�����ABCD�ı�����ʱ��ֻ�е�O���D�غ�ʱ���ڣ���ʱ��O�뾶r��CD��4����COF��90�㣬�����������ʽ���ɵó����
��1���⣺��Cһ������O�ϵ��������£�
����OC����ͼ��ʾ��
����ת�����ʵã���ECF��90�㣬
��EF����O��ֱ����OΪԲ�ģ�
��OE��OF��
��OC��OE��OF��
���Cһ������O�ϣ�
��2��֤��������ת�����ʵã���ECF��90�㣬CE��CF��
��OE��OF��
��CO��EF��
��MCΪ��O��ֱ����
��CM��EF��OC��OM����MEC��90�㣬
��EM��CE��
����M��MN��AD��N����ͼ��ʾ��

�ߡ�DEC+��DCE��90�㣬��DEC+��DEM��90�㣬
���DEM����DCE��
�ڡ�MEN�͡�CED�У�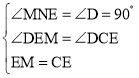 ��
��
���MEN�ա�CED��AAS����
��MN��DE������M��AD�ľ�������߶�DE�ij���
��3���⣺�ߵ�E�ھ���ABCD�ı�AD�ϣ�AD��6��
���D��90�㣬��AE��x����DE��6��x��
�ɣ�2���ã���M��AD�ľ�������߶�DE�ij���
��S��AEM��![]() ��x����6��x������
��x����6��x������![]() x2+3x����
x2+3x����![]() ��x��3��2+
��x��3��2+![]() ��
��
�൱x��3ʱ����AEM���ȡ�����ֵ![]() ��
��
��ʱ��DE��6��3��3��
��tan��ACD��![]() ��
��![]() ��
��
��CD��![]() ��4��
��4��
�ɹ��ɶ����ã�CE2��DE2+CD2����CE2��32+42��
��CE��5��
�ɣ�2���ã�CM��EF��OC��OM����MEC��90�㣬
���CEF��45�㣬
��Rt��CEF��EF��![]() ��
��![]() ��5
��5![]() ��
��
����O�뾶�ij�Ϊ![]()
![]() ��
��
��4������O�����ABCD�ı�����ʱ��ֻ�е�O���D�غ�ʱ���ڣ���ʱ��O�뾶r��CD��4����COF��90�㣬S��OCF=![]() ��4����
��4����

 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�