题目内容
【题目】如图,![]() .
.

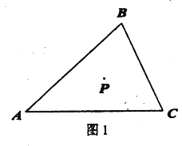
(1)如图①,在平面直角坐标系中,以![]() 为顶点,
为顶点,![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() ,若
,若![]() ,求
,求![]() 点的坐标;
点的坐标;
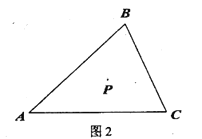
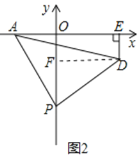
(2)如图②,![]() 为
为![]() 轴负半轴上一个动点,以
轴负半轴上一个动点,以![]() 为顶点,
为顶点,![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,当
点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,试问
轴负半轴向下运动时,试问![]() 的值是否发生变化?若不变,求其值,若变化,请说明理由;
的值是否发生变化?若不变,求其值,若变化,请说明理由;
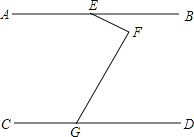
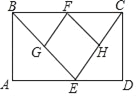
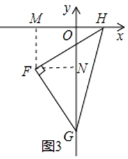
(3)如图③,已知点![]() 坐标为
坐标为![]() ,
,![]() 是
是![]() 轴负半轴上一点,以
轴负半轴上一点,以![]() 为直角边作等腰
为直角边作等腰![]() ,
,![]() 点在
点在![]() 轴上,
轴上,![]() ,设
,设![]() 、
、![]() ,当
,当![]() 点在
点在![]() 轴的负半轴上沿负方向运动时,
轴的负半轴上沿负方向运动时,![]() 的和是否发生变化?若不变,求其值;若变化,请说明理由.
的和是否发生变化?若不变,求其值;若变化,请说明理由.
【答案】(1)C点的坐标为(-6,-2);(2)OP-DE的值不变,值为2;(3)m+n的和不变,值为-8.
【解析】
(1)作CD⊥x轴于D,证明△ACD≌△BAO,根据全等三角形的性质得到DC=OA=2,AD=OB=4,计算即可;
(2)作DF⊥y轴于F,证明△APO≌△DPF,得到PF=OA=2,DF=OP,结合图形计算;
(3)作PM⊥x轴于M,PN⊥y轴于N,仿照(2)的证明过程解答.
解:(1)作CD⊥x轴于D,

∴∠ACD+∠CAD=90°,
∵∠CAB=90°,
∴∠BAO+∠CAD=90°,
∴∠BAO=∠ACD,
在△ACD和△BAO中,
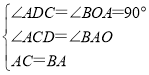 ,
,
∴△ACD≌△BAO,
∴DC=OA=2,AD=OB=4,
∴OD=6,
∴C点的坐标为(-6,-2);
(2)OP-DE的值不变,值为2,
理由如下:作DF⊥y轴于F,
∴∠PDF+∠DPF=90°,
∵∠APD=90°,
∴∠APO+∠DPF=90°,
∴∠APO=∠PDF,
在△APO和△DPF中,
 ,
,
∴△APO≌△DPF,
∴PF=OA=2,DF=OP,
∴OP-DE=OP-OF=PF=2;
(3)m+n的和不变,值为-8,
理由如下:作PM⊥x轴于M,PN⊥y轴于N,
由(2)可知,△HNF≌△GNF,
∴GN=MH,FN=FM=OM=4,
m+n=-(OG-OH)=-(GN+ON-MH+OM)=-(ON+OM)=-8.
故答案为:(1)C点的坐标为(-6,-2);(2)OP-DE的值不变,值为2;(3)m+n的和不变,值为-8.

【题目】滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.8元/公里 | 0.45元/分钟 | 0.4元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元. | |||
(1)若小东乘坐滴滴快车,行车里程为20公里,行车时间为30分钟,则需付车费________元.
(2)若小明乘坐滴滴快车,行车里程为a公里,行车时间为b分钟,则小明应付车费多少元(用含a、b的代数式表示,并化简.)
(3)小王与小张各自乘坐滴滴快车,行车里程分别为9.5公里与14.5公里,如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差多少分钟?
【题目】某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为![]() ~
~![]() 的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
的产品为合格〉.随机各抽取了20个祥品迸行检测.过程如下:
收集数据(单位:![]() ):
):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.
整理数据:
组别频数 | 165.5~170.5 | 170.5~175.5 | 175.5~180.5 | 180.5~185.5 | 185.5~190.5 | 190.5~195.5 |
甲车间 | 2 | 4 | 5 | 6 | 2 | 1 |
乙车间 | 1 | 2 |
|
| 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | 180 | 22.6 |
应用数据;
(1)计算甲车间样品的合格率.
(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.