题目内容
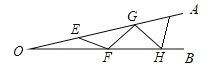
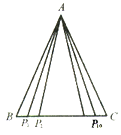
【题目】如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过圆锥底面圆的圆心,圆锥的高为2![]() m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
m,底面半径为2 m,某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4 m.
(1)求∠ABC的度数;
(2)若∠ACP=2∠ABC,求光源A距水平面的高度.

【答案】(1)∠ABC=30°;(2)4![]() m.
m.
【解析】(1),过点D作DF垂直BC于点F,则在Rt△DFB中,运用正切函数tan∠B=DFBF,即可以求出∠ABC的度数;
(2),结合已知条件∠ACP=2∠B以及三角形的外角性质,可求出∠BAC=30 °,进而依据等角对等边可得AC=BC=8,过点A作AH垂直BP于点H构造Rt△ACH,并在直角三角形中运用正弦函数可求出AH=ACSin∠ACP,至此本题可解.
(1)如图,过点D作DF⊥BC于点F.
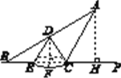
由题意,得DF=2![]() m,EF=2 m,BE=4 m.
m,EF=2 m,BE=4 m.
在Rt△DFB中,BF=BE+EF=4+2=6(m),
∴DB=![]() =
=![]() =4
=4![]() (m),
(m),
∴DF=![]() DB,
DB,
∴∠ABC=30°.
(2)如图,过点A作AH⊥BP,垂足为H.
∵∠ACP=2∠ABC=60°,
∴∠BAC=30°,
∴AC=BC=8 m.
在Rt△ACH中,AH=8sin60°=8×![]() =4
=4![]() (m),即光源A距水平面的高度为4
(m),即光源A距水平面的高度为4![]() m.
m.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目